|
|
|
| |
| ABSTRACT |
|
The purpose of this study was to analyze if different combinations of trials as well as mathematical models can modify the aerobic and anaerobic estimates from critical velocity protocol applied in canoe slalom. Fourteen male elite slalom kayakers from Brazilian canoe slalom team (K1) were evaluated. Athletes were submitted to four predictive trials of 150, 300, 450 and 600 meters in a lake and the time to complete each trial was recorded. Critical velocity (CV-aerobic parameter) and anaerobic paddling capacity (APC-anaerobic parameter) were obtained by three mathematical models (Linear1=distance-time; Linear 2=velocity-1/time and Non-Linear = time-velocity). Linear 1 was chosen for comparison of predictive trials combinations. Standard combination (SC) was considered as the four trials (150, 300, 450 and 600 m). High fits of regression were obtained from all mathematical models (range - R² = 0.96-1.00). Repeated measures ANOVA pointed out differences of all mathematical models for CV (p = 0.006) and APC (p = 0.016) as well as R² (p = 0.033). Estimates obtained from the first (1) and the fourth (4) predictive trials (150 m = lowest; and 600 m = highest, respectively) were similar and highly correlated (r=0.98 for CV and r = 0.96 for APC) with the SC. In summary, methodological aspects must be considered in critical velocity application in canoe slalom, since different combinations of trials as well as mathematical models resulted in different aerobic and anaerobic estimates. |
| Key words:
Canoe slalom, critical velocity, sports performance, aerobic parameter, anaerobic parameter, elite athletes
|
Key
Points
- Great attention must be given for methodological concerns regarding critical velocity protocol applied on canoe slalom, since different estimates were obtained depending on the mathematical model and the predictive trials used.
- Linear 1 showed the best fits of regression. Furthermore, to the best of our knowledge and considering practical applications, this model is the easiest one to calculate the estimates from critical velocity protocol. Considering this, the abyss between science and practice may be decreased. Coaches of canoe slalom may simply apply critical velocity protocol and calculate by themselves the aerobic and anaerobic estimates.
- Still considering practical application, the results of this study showed the possibility of calculating the critical velocity estimates by using just two trials. These results are extremely relevant regarding saving time and easy applicability of this protocol for canoe slalom.
|
Critical power protocol was firstly applied in monoarticular exercise (Monod and Scherrer, 1965), and subsequently adapted to whole-body (Moritani et al., 1981). This protocol is based in mathematical analysis using the intensity/time relationship from 2 to 5 exhaustive trials. With this approach, it is possible to obtain an anaerobic estimate (critical power - CP) as well as an anaerobic estimate (anaerobic work capacity - AWC), which are highly associated to physiological responses (Jones et al., 2010). Additionally, Jones et al. (2010) recently emphasized that the CP is related to the intensity of transition between the heavy and severe intensity domains. Different mathematical models have been used to analyze the critical power for humans on cycle ergometer (Bull et al., 2000) and treadmill (Bergstrom et al., 2014; Housh et al., 1990; 2001; Smith et al., 2011) and even until for rodents submitted to swimming (Gobatto et al., 2013) and treadmill running exercise (Copp et al., 2010). However, there are evidences that despite mathematical equivalents (Jones et al., 2010), they do not necessarily result in similar aerobic and anaerobic estimates (Gaesser et al., 1995; Gobatto et al., 2013). Besides, authors have been proposing that some factors, such as numbers of bouts (Housh et al., 1990; Kennedy and Bell 2000; Smith et al., 2011) and time to exhaustion (Bishop et al., 1998) could result in different aerobic and anaerobic estimates. Despite extensively explored in many types of exercises (Fukuda et al., 2012; Kennedy and Bell 2000; Wakayoshi et al., 1992; Zagatto and Gobatto 2012), the critical velocity protocol (i.e analogous of critical power protocol) has been investigated in slalom kayakers (Manchado-Gobatto et al., 2014). Nonetheless, there is no information regarding mathematical modeling analysis and number of predictive trials on critical velocity protocol using the relationship between distance covered (D) and time to cover the distance (T) (D'-T' model) (Lloyd, 1966; Kenedy and Bell, 2000; Manchado-Gobatto et al., 2014). By this application, the critical velocity (i. e analogous of critical power) and the anaerobic paddling capacity (i. e analogous of anaerobic work capacity) estimates can be analyzed considering methodology aspects. It is noteworthy that the reliable parameters determination considering these factors are of utmost relevance, both for assessing aerobic and anaerobic estimates as well as for prescribing exercise intensity based on these parameters. Additionally, taking on practical applications, the analysis of different mathematical models and trials combinations can result in high applicability and saving time on determination of aerobic and anaerobic estimates. Therefore, the aim of this study was to analyze if different combinations of predictive trials as well as mathematical models can result in different aerobic and anaerobic estimates of slalom kayakers through the application of critical velocity protocol. ParticipantsFourteen elite athletes (national Brazilian team level, K1 category, age 18 ± 3 years, body mass 68.1 ± 0.6 kg, height 1.74 ± (0.06) m; fat body 10.3 ± 0.1 %, Somatotype – Endomorph 3.2 / Mesomorph 3.9 / Ectomorph 2.3) were evaluated. 50% of athletes participated of the canoe slalom World Cup in 2013, and 69% were classified in the canoe slalom world ranking according to the International Canoe Federation (ICF). Athletes and parents were informed about the risks of the experimental procedures, and both provided written, informed consent authorizing the athlete’s participation in this study. All experiments were approved by the Local Ethic Committee and were conducted in accordance with the ethics of the declaration of Helsinki.
Critical velocity protocolAthletes were submitted to four trials of paddling on distances equivalents to 150, 300, 450 and 600 meters in a lake (Itaipu plant, Foz do Iguaçu-PR, Brazil). Trials were conducted in two days, randomly, with five hours of interval between them. Distances were marked using four buoys, two positioned at the starting point and two at the finish line, and the time required to cover distances was recorded with a stopwatch (HS-30W-N1V-CASIO).
Mathematical analysis of critical velocity protocolConsidering data from the critical velocity protocol, three mathematical models were applied for the analysis of critical velocity (CV) and anaerobic paddling capacity (APC):
Linear 1 consists in the relationship between the total distance covered (D) and total time to cover the distance (T) (Lloyd, 1966; Kennedy and Bell, 2000; Manchado-Gobatto et al., 2014) (Equation 1). The CV is related to slope of regression and APC to intercept-y (Figure 1a).
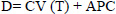 |
Equation 1 |
Linear 2 consists in the relationship between the mean velocity (MV) and inverse of time (1/T) (Wakayoshi et al., 1992) (Equation 2). The CV is related to the intercept-y and the APC to slope of regression (Figure 1b).
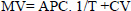 |
Equation 2 |
Non-Linear (Equation 3) consists in the hyperbolic relationship between the total time to cover the distance (T) and the mean velocity (MV). The CV is equivalent to the asymptote of x axis, and APC to the slope of regression (Figure 1c).
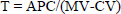 |
Equation 3 |
Combination of predictive trialsDifferent combinations of predictive trials were used in the analysis of critical velocity estimates. Trials of 150, 300, 450 and 600 m corresponded to numbers 1, 2, 3 and 4, respectively. With this approach, all possible combinations made by two or three predictive trials were accomplished. The standard combination (SC) was considered as the four predictive trials.
Statistical analysisStatistical analysis was carried out using a statistical software package (Statistic 7.0, Statsoft, Tulsa, USA). Mean and standard deviation were calculated for all studied variable. After checking for data normality and sphericity using Shapiro-Wilk's and Mauchly's tests, respectively, the one-way repeated measures ANOVA was applied for comparisons of mathematics models and trials combinations. Huynh-Feldt correction for degrees of freedom and Scheffe's post hoc test were employed when pertinent. Coefficient of determination (R2) was calculated as indexes of fitting adjustments for the different mathematical models. Pearson product moment correlation was employed for relationship analysis. Bland-Altman’s analysis was used to assess the agreement between different trials combinations. Accuracy and precision definition were according Bland and Altman, (1986) criteria. Coefficient of variation and percentage difference between means were calculated considering the criteria established by Hopkins et al., (2001). In all cases, statistical significance was set at p < 0.05.
Regarding the times to complete the predictive trials, a range between 1 and 5 minutes was visualized, being the mean time for the shortest (150 m) and the longest (600 m) trials relative to 50.64 ± 5.21 s and 259.64 ± 12.86 s, respectively (Figure 2). In relation of the comparison between CV and APC from mathematical models, no difference was visualized between Linear 1 and other models. On the other hand, differences were found between Linear 2 and Non-Linear. In regard of fitting adjustments, the Linear 1 model resulted in the highest R² (R² = 0.99) (Table 1). Due to the highest R² obtained in Linear 1 model, this mathematical approach was chosen for the comparison between SC and all possible combinations (Table 2). ANOVA indicated no differences for CV. Yet, for APC, only the combination of 2 and 3 were different. Table 3 shows the results for the limits of agreement, coefficient of variation and difference in percentage among means for SC and all other combinations. For CV, all combinations showed high precision and accuracy (from 0.12 ± 0.47 to 0.13 ± 0.46). Additionally, low coefficient of variation (from 0.23% to 4.09%) and percentage difference between means (from 5.67% to 5.89%) were observed. However, for APC, only the combination of 1, 2 and 4 (-0.16 ± 3.39) showed precision and accuracy in comparison to SC. Besides, low coefficient of variation and percentage difference between means were observed for 1, 2 and 3 (0.14% and -4.04% respectively) and 1, 2 and 4 (1.39% and -0.36 respectively). Widely studied, the critical power protocol is considered as a marker of metabolic transition predominance. Furthermore, this protocol provides an inestimable value on the understandings of fatigue mechanisms and exercise intolerance (Jones et al., 2010). The critical power model was initially described by Monod and Scherrer (1965). These authors showed that for monoarticular exercises, a linear relationship between intensity and time to exhaustion is obtained. Thereafter, Lloyd, 1966 showed that the distances (d) of world records in running increase linearly with record times (t), proposing an analogous of critical power for the relationship between distance and time to cover the distance (i.e critical velocity model) (Di Prampero et al., 2007). Despite the fact that Manchado-Gobatto et al., (2014) have showed the effect of training in critical velocity estimates for slalom kayakers, the methodological analysis of this protocol in nautical sports was originally explored on kayak ergometer by Clingeleffer et al. (1994). Hence, Kennedy and Bell (2000) applied the critical velocity protocol and studied different mathematical models in rowing. Despite the original findings of these studies, there is a lack of detailed information about methodological aspects in canoe slalom. Regarding comparisons between mathematical models, we found that Linear 2 and Non-Linear provided different estimates. In part, our results agree with Kennedy and Bell (2000). However, comparisons between our results (i.e. values) on this topic are not straight forward due to markedly differences in the modalities features and methodological aspects. Moreover, our data corroborates with the literature, since it is well established that, although mathematically equivalent, different mathematical modeling does not produce similar estimates for critical power (Bergstrom et al., 2014; Bull et al., 2000; Gaesser et al., 1995; Hill 1993) and critical velocity protocols (Housh et al., 2001). Monod and Scherrer (1965) previously demonstrated that only two predictive trials could competently estimate aerobic and anaerobic parameters. In accordance, Housh et al., (1990) showed that critical power analyzed by two predictive trials (the lowest and highest) can promote similar estimates to standard combination based on four predictive trials. Kennedy and Bell (2000), related that predictive trials using distances of 400, 600, 800 and 1000 m provided similar estimates to a standard combination based on six predictive trials (200, 400, 600, 800, 1000 and 1200 m). Similarly, Clingeleffer et al., (1994) found that combinations using the shortest (90s) and the longest (1200s) times promoted similar estimates to a standard combination of four predictive trials (90, 240, 600 and 1200 s). In agreement with all studies, we observed that estimates obtained by the SC (1, 2, 3 and 4) were not different and were highly correlated with the combination of the shortest and highest trials (1 and 4) (Table 2). Additionally, for CV, the combination of 1 and 4 was highly precise and accurate (-0.01±0.23) according to Bland and Altman, (1986) analysis. Furthermore, the other combinations of two and three predictive trials were not different and were correlated with the SC. Only the combination of 2 and 3 showed poor correlation with CV. For APC, only the combination of 2 and 3 was different from APC. Additionally, most of APC combinations showed poor accuracy, precision, coefficient of variation and difference between means when compared with SC. Is valid to state that when some combinations of trials showed difference and poor agreement with SC, the range of times to cover the distance was lower than 74 seconds? In that sense, it is suggested that when the range of time between predictive trials is greater than ~74s, only two and three predictive trials can be used to obtain reliable CV and APC estimates. This debate leads to a controversial discussion regarding the number of necessary predictive trials as well as the range time to exhaustion/cover the distance that have to be considered in critical power/velocity protocols. Poole (1986) suggested that in order to secure realistic slope and y-intercept, it is necessary to obtain 4 or 5 tests with times ranging between 1 and 10 minutes. In parts, Housh et al., (1990) agreed with this, however they conclude that only two tests could predict realistic estimates if times differ by approximately 5 minutes. Recently, Jones et al., (2008) considered 3 or 4 trials with a range between 2 and 15 minutes. In fact, divergences between the numbers of tests (i.e. predictive trials) as well as the range of times may lead to a protocol dependency, resulting in ambiguous interpretations. In an attempt to understand this, Bishop et al., (1998) emphasized the “one-compartment” model of human bioenergetics, stressing that this protocol dependency may be due to the “aerobic inertia” effect during the predictive trials. To minimize this effect, Bishop proposed that range of times from predictive trials should be at least greater than 3 minutes (where the aerobic contribution in near maximal rates i.e. VO2max) and not greater than 20 minutes (to avoid effects of diet, hydration, temperature and motivation). Although the range of time in this study does not engage in Bishop assumption, it is valid to state that predictive trials distances were chosen considering the similarities of metabolic supply according to canoe slalom races specificity. In general, despite of largely explored in different modalities, critical velocity protocol was only analyzed for effect of training on aerobic and anaerobic parameters (Manchado-Gobatto et al., 2014), however this is the first study regarding methodological concerns for critical velocity protocol in canoe slalom. Additionally, in canoe slalom this proposal is essential to optimize the performance of these athletes. Besides, the critical velocity protocol is a non-invasive and inexpensive protocol, and it can be applied in field preserving the sport specificity. In that sense, with only a stopwatch and a demarcated distance, coaches and researchers can obtain aerobic and anaerobic estimates, which can clearly be used for training prescription and intensity control. Regarding the methodological concerns in critical velocity protocol for canoe slalom, the present investigation showed that high R² values were obtained using linear and non-linear models in critical velocity protocol application. Additionally, it is possible to suggest that if the range of times was greater than ~74 seconds, only two or three predictive trials are necessary to provide reliable aerobic and anaerobic estimates. In this sense, the main advantage of using fewer trials in critical velocity protocol may result in time saving and improved applicability for coaches and researchers.
| ACKNOWLEDGEMENTS |
We would like to thank the coaches and athletes of national Brazilian team of canoe slalom. Also thank to the Fundação de Amparo à Pesquisa do Estado de São Paulo (FAPESP – Proc. 2012/06355-2 and 2009/08535-5), Conselho Nacional de Desenvolvimento Científico e Tecnológico (CNPq - Proc. 472277/2011-1), Fundo de Apoio ao Ensino, à Pesquisa e à Extensão (FAEPEX – Proc. 756/13), and Funcamp (Proc. 1403) for financial support. |
|
| AUTHOR BIOGRAPHY |
|
 |
Leonardo H. D. Messias |
| Employment: PhD Student |
| Degree: Master |
| Research interests: Exercise physiology, Physical Training |
| E-mail: leo.137@hotmail.com |
| |
 |
Homero G. Ferrari |
| Employment: Professor |
| Degree: PhD |
| Research interests: Exercise physiology, Physical Training |
| E-mail: hgferrari@ig.com.br |
| |
 |
Ivan G. M. Reis |
| Employment: PhD Student |
| Degree: Master |
| Research interests: Exercise physiology, Physical Training |
| E-mail: ivanbarizom@hotmail.com |
| |
 |
Pedro P. M. Scariot |
| Employment: PhD Student |
| Degree: Master |
| Research interests: Exercise physiology, Physical Training |
| E-mail: pedroppms@yahoo.com.br |
| |
 |
Fúlvia B. Manchado-Gobatto |
| Employment: Professor |
| Degree: PhD |
| Research interests: Exercise physiology, Physical Training |
| E-mail: fbmanchado@yahoo.com.br |
| |
|
| |
| REFERENCES |
 Bergstrom H.C., Housh T.J., Zuniga J.M., Traylor D.A., Lewis R.W., Camic C.L., Johnson G.O. (2014) Differences among estimates of critical power and anaerobic work capacity derived from five mathematical models and the three-minute all-out test. TheJournal of Strength and Conditioning Research 28, 592-600. |
 Bishop D., Jenkins D. G., Howard A. (1998) The Critical Power Function is Dependent on the Duration of the Predictive Exercise Tests Chosen. lnternational ]ournal of Sports Medicine 19, 4-. |
 Bland J.M., Altman D.G. (1986) Statistical methods for assessing agreement between two methods of clinical measurement. Lancet 1, 307-310. |
 Bull A.J., Housh T.J., Johnson G.O., Perry S.R. (2000) Effect of mathematical modeling on the estimation of critical power. Medicineand Science in Sports and Exercise 32, 526-530. |
 Clingeleffer A., McNaughton L., Davoren B. (1994) Critical power may be determined from two tests in elite kayakers. European Journalof Applied Physiologyand Occupational Physiology 68, 36-40. |
 Copp S.W., Hirai D.M., Musch T.I., Poole D.C. (2010) Critical speed in the rat: implications for hindlimb muscle blood flow distribution and fibre recruitment. Journal of Physiology 588, 5077-5087. |
 Di Prampero P.E., Dekerle J., Capelli C., Zamparo P. (2007) The critical velocity in swimming. European Journal of Applied Physiology 102, 165-171. |
 Fukuda D.H., Smith A.E., Kendall K.L., Hetrick R.P., Hames R.L., Cramer J.T., Stout J.R. (2012) The reliability of the intermittent critical velocity test and assessment of critical rest interval in men and women. European Journalof Applied Physiology 112, 1197-1205. |
 Gaesser G.A., Carnevale T.J., Garfinkel A., Walter D.O., Womack C.J. (1995) Estimation of critical power with nonlinear and linear models. Medicineand Science in Sports and Exercise 27, 1430-1438. |
 Gobatto C.A., Scariot P.P.M., Ribeiro L.F.P., Manchado-Gobatto F.B. (2013) Critical load estimation in young swimming rats using hyperbolic and linear models. Comparative Exercise Physiology 9, 85-91. |
 Hill D.W. (1993) The critical power concept. A review. Sports Medicine 16, 237-254. |
 Hopkins W.G., Scharbort E.J., Hawley J.A. (2001) Reliability of power in physical performance tests. Sports Medicine 31, 211-234. |
 Housh D.J., Housh T.J., Bauge S.M. (1990) A methodological consideration for the determination of critical power and anaerobic work capacity. Research Quartely for Exercise and Sport 61, 406-409. |
 Housh T.J., Cramer J.T., Bull A.J., Johnson G.O., Housh D.J. (2001) The effect of mathematical modeling on critical velocity. European Journalof Applied Physiology 84, 469-475. |
 Hughson R.L., Orok C.J., Staudt L.E. (1984) A high velocity treadmill running test to assess endurance running potential. International Journal of Sports Medicine 5, 23-25. |
 Jones A.M., Vanhatalo A., Burnley M., Morton R. H., Poole D.C. (2010) Critical power: implications for determination of VO2max and exercise tolerance. Medicine and Science in Sports and Exercise 42, 1876-1890. |
 Jones A.M., Wilkerson D.P., DiMenna F., Fulford J., Poole D.C. (2008) Muscle metabolic responses to exercise above and below the “critical power” assessed using 31P-MRS. The American Journal of Physiology - Regulatory, Integrative and Comparative Physiology 294, 585-593. |
 Kennedy M.D.J., Bell G.J. (2000) A comparison of critical velocity estimates to actual velocities in predicting simulated rowing performance. Canadian Journal of Applied Physiology 25, 12-. |
 Lloyd B.B. (1966) The energetics of running: an analysis of world records. Advancement of Science 22, 15-. |
 Manchado-Gobatto F.B., Vieira N.A., Messias L.H.D., Ferrari H.G., Borin J.P., Andrade V.C., Terezani D.R. (2014) Anaerobic threshold and critical velocity parameters determined by specific tests of canoe slalom:Effects of monitored training. Science and Sports 29, 55-58. |
 Messias L.H.D., Reis I.M., Ferrari H.G., Manchado-Gobatto F.B. (2014) Physiological, psychological and biomechanical parameters applied in canoe slalom training: a review. International Journal of Performance Analysis in Sport 14, 24-41. |
 Monod H., Scherrer J. (1965) The work capacity of a synergic muscular group. Ergonomics 8, 329-338. |
 Moritani T., Nagata A., deVries H. A., Muro M. (1981) Critical power as a measure of physical work capacity and anaerobic threshold. Ergonomics 24, 339-350. |
 Poole D.C. (1986) Measurements of the anaerobic work capacity in a group of highly trained runners. Medicineand Science in Sports and Exercise 18, 703-705. |
 Smith A.E., Kendall K.L., Fukuda D.H., Cramer J.T., Stout J.R. (2011) Determination of aerobic and anaerobic performance: a methodological consideration. Physiological Measurement 32, 423-431. |
 Wakayoshi K., Ikuta K., Yoshida T., Udo M., Moritani T., Mutoh Y., Miyashita M. (1992) Determination and validity of critical velocity as an index of swimming performance in the competitive swimmer. European Journalof Applied Physiologyand Occupational Physiology 64, 153-157. |
 Zagatto A.M., Gobatto C.A. (2012) Relationship between anaerobic parameters provided from MAOD and critical power model in specific table tennis test. International Journal of Sports Medicine 33, 613-620. |
|
| |
|
|
|
|

