|
|
|
| |
| ABSTRACT |
|
In the frontal crawl, the propulsive action of the limbs causes lateral fluctuations from the straight path, which can be theoretically seen as the best time saving path of the race. The purpose of the present work was to analyze the head trajectory of 10 elite athletes, during a competition of 400 m front crawl, in order to give information regarding the path linearity of elite swimmers. The kinematic analysis of the head trajectories was performed by means of stereo-photogrammetry. Results showed that the forward speed and lateral fluctuations speed are linearly related. Multiple regression analysis of discrete Fourier transformation allowed to distinguish 3 spectral windows identifying 3 specific features: strokes (0.7-5 Hz), breathings (0.4-0.7 Hz), and voluntary adjustments (0-0.4 Hz), which contributed to the energy wasting for 55%, 10%, and 35%, respectively. Both elite swimmers race speed and speed wastage increase while progressing from the 1st to the 8th length during a 400 m front crawl official competition. The main sources of the lateral fluctuations that lead to the increasing speed wastage could be significantly attributed to strokes and voluntary adjustments, while breathings contribution did not reach statistical significance. In conclusion, both strokes and voluntary adjustments are the main energy consuming events that affect path linearity. |
| Key words:
Drift, lateral fluctuations, video analysis, performance assessment, swimming
|
Key
Points
- The lateral fluctuations (LF) represent indexes of elite performance swimmers during 400 m competitions.
- The voluntary adjustments needed to go back to the ideal trajectory are more energy consuming than the movements of the swimmer for maintaining the path linearity.
- The diverge from the ideal swimming trajectory during a high level competition explain about 14.7% of the variations of the average forward velocity during the race.
|
The maximum speed of swim depends on the equilibrium between the drag and the propulsive energy. The drag is directly related to the body frontal area contrasting the forward motion and represents a limiting factor of elite performances (Zamparo et al., 2012). It grows exponentially with increasing velocity (Toussaint and Hollander, 1994) and can be affected by several factors, some of which have never been considered until recently (i.e. the characteristics of the swim cup) (Gatta et al., 2013). One of the most effective strategy to reduce drag is maintaining the body position as much hydrodynamic as possible during the propulsive action (Clarys, 1979). During swimming, also non-propulsive forces are generated. Those forces produce a series of rotations around the reference spatial axes (Yanai, 2003) that are substantially ineffective to the forward motion of the swimmer and are mainly due to the feature of the technique components, included breathing frequency (Seifert et al., 2004), and to the fatigued condition of the swimmer (Aujouannet et al., 2006). These rotations often affect the swimmer’s attitude, generating a non-optimal hydrodynamic position due to an increase of the body frontal area and thus of the active drag (Maglischo, 2003). The body movements ineffective to the forward motion lead to an energy wastage that is related to the amplitude of the oscillations around the ideal trajectory, with predictable negative consequences on performance. Therefore, one can hypothesize that the lower the technical skill, the more the swimmers are expected to diverge from the faster and more favorable progress line, thus increasing both distance swam and race time. For this reason, during the training sessions coaches usually correct the swimmer movements in order to maintain the linearity during the forward motion. However, it is difficult to define the value above which it is necessary to give indications to the swimmer and to which extent is possible to correct these oscillations. The deviations of the swimmer attitude, which can occur around 3 axes, are commonly classified in: rolls, pitches and yaws. Besides body roll and pitch angles, which are typical of either asymmetric or symmetric strokes, respectively, the body yaw angles occur in both symmetric and asymmetric strokes and can largely affect the path linearity of swim. In a pilot study, the instantaneous lateral-medial displacements, away from or toward of the midline of the lane (namely lateral fluctuations, LF), and the overall drift from a straight path, were assessed for the first time in 25 m front crawl trials at different velocities, analyzing the swimmers head trajectory by means of stereo-photogrammetry (Gatta et al., 2008). Briefly, stereo-photogrammetry allows the reconstruction of the three-dimensional position of a marker by means of triangulation, which can be performed when, after the calibration of the field of view, two cameras identify the same marker. The results showed a lower energy dissipation for LF in higher level athletes and a lower overall drift with training velocity between 80% and 90% of maximal speed, compared to lower level athletes. As hypothesized, LF were found to contribute to increase drag because the swimmer body take up more space and disrupt laminar flow. However, the overall drift may be considered negligible when considering short-distance swimming events (Gatta et al., 2008). To the best of our knowledge, nobody has investigated the body yaw angles of elite athletes during long-distance, high level, official competitions, thus in the actual conditions of the race. The aim of the present work was twofold: firstly, to obtain the model of the path linearity of the center of the head in elite athletes during an official competition of 400 m front crawl (Italian Swimming Championship); secondly, to give useful information regarding path linearity of swimming to the coaches of high level athletes. SubjectsThe present study evaluated 10 elite male swimmers (age: 23 ± 4.2 years; body mass: 78.0 ± 3.8 kg; height: 1.85 ± 0.05 m) at the 2009 Italian Swimming Championship. All subjects had experience in International swimming competitions and their race times (400 m front-crawl) ranged between 3†²47.45†³ and 3†²57.56†³. The Italian Swimming Federation gave a written permission to film all the athletes during the competition. The project was approved by the local Ethics committee and all participants signed an informed consent form to participate in the study before the competition.
ProceduresIn order to evaluate swimmers trajectories, the races were video-recorded and later analysis were performed on the row material recorded. The 3rd and 4th lanes of 400 m front crawl stroke were analyzed. The number of lanes acquired was restricted to 2 due to the limited space available to situate the cameras. All the races were filmed by 2 synchronized digital cameras (Sony Dcr-Hc1000, Tokyo, Japan). The sampling rate of video recordings was 50 Hz. Cameras were placed beside the 50 m swimming pool at 6 m high with respect to the water surface (Figure 1). The central part of the swimming pool, corresponding to 40 m, was analyzed excluding the underwater phases (starting, flip turning and pushing from the wall) and considered in the present study as the length. The underwater phases were not taken into account, as they are not related to the stroke technique. A reference system was defined as follows: the origin at the beginning of volume of acquisition near the 4th lane, the X-axis corresponds to the medio-lateral fluctuations, the Y-axis corresponds to the direction of swim, and the Z-axis corresponds to the vertical axis (Figure 1). The calibration of the acquisition field was performed by means of a virtual parallelepiped, 5 m wide (X-axis), 40 m long (Y-axis), and 1 m high (Z-axis). The parallelepiped was defined by 2 virtual panels, at the beginning and at the end of the central part of the lane, and by 12 uniformly distributed buoys with a diameter of 0.08 m. The calibration volume, visible from both cameras, was acquired before the competition. The consistency of the calibration procedure showed a difference between the 2D coordinates of the calibration points and the 3D coordinates of the same points re-projected into the camera image lower than 10% with respect to the length of the longer side of the camera image (width 768 pixels, height 576 pixels, resolution 37.8 pixels/cm). The head of the swimmer was identified and digitized by the same operator on each frame of the video using a commercial software (SIMI Reality Motion System GmbH – version 7, Unterschleissheim, Germany). The head, as discussed elsewhere (Gatta et al., 2008), allows an accurate identification of the swimmer trajectory thanks to the high visibility during the whole central part of the swimming pool. From the 2D coordinates digitized on the image plane of each calibrated camera, the 3D coordinates of the swimmers head were reconstructed. According to Canny (1986) and Cappozzo (1984), the estimation of the centre of the head was made by: i) extracting the swim-cap contour by means of a semi-automated procedure, and ii) considering the centre of the head as the centre of the circle fitted to the edge points in least-square sense.
Statistical analysisFirstly, a regression line was calculated on the LF of the head of each swimmer and its slope compared to the ideal swimming trajectory (i.e. slope = 0). Secondly, the discrete Fourier transformation (DFT) analysis of detrendized LF displacements was used to quantify the amount of dissipated energy due to LF. LF were preliminarily detrendized by subtracting the regression line of the path of the swimmer to the relative time serie. This equals to zero the overall mean of the LF time series, thus allowing to perform a DFT analysis by using LF that ideally start from the same spatial coordinates for each swimmer. The DFT transforms the time series of the detrendized LF in sums of spectral harmonics; each spectral harmonic was defined according to Equation 1:
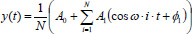 |
Equation 1 |
where t is the sampling time, N is the total number of LF sampled, i is the number of harmonics, A0 is the mean amplitude and A1 is the amplitude of the i-esim harmonic, ω is the harmonic, and Ï•1 is the phase. The power of temporal series (Parseval’s theorem) equals the sum of square of amplitude of the single Fourier harmonics. Parseval’s theorem is a kind of energy-conservation theorem, which states that a signal contains a given amount of energy regardless of whether that energy is computed in the space/time domain or in the Fourier/frequency domain. Details on this statistics can be found in Pocock (1974). Since elite athletes have similar characteristics (such as body volume and composition) and comparable race speeds, one can assume that these factors have similar and negligible effects on active drag. In turn, the only remaining factor affecting active drag, which is energy consuming but does not lead to the forward motion of the swimmer, is represented by LF. Obviously, the assumption does not allow a straight determination of the amount of dissipated energy, but an estimation is still possible. Similarly to another study performing the spectral analysis of breathing and stroke frequency in relation to hearth rate variability during swimming (Di Michele et al., 2011), we then conducted a spectral analysis of the variable that describes the path linearity, i.e. LF. The Fourier series were truncated at the 20th harmonic (with a 7 Hz low-pass filter) since no technical event in front-crawl swimming can be performed with the upper part of the body in a period shorter than 0.2 s (i.e. >5 Hz), and were split in the spectral windows of 0.7-5 Hz, 0.4-0.7 Hz, and 0-0.4 Hz, which represent time frames of 0.2-1.4 s, 1.4-2.5 s, and >2.5 s, respectively. These spectral windows were chosen according to the time needed to perform the technical events of ‘stroke’ (0.2-1.4 s) and ‘respiration’ (1.4-2.5 s). Both parameters were derived from available literature (Payton et al., 1999) and from the video-analysis of this study data, i.e. averaging the times the swimmers took to perform those technical events. The video-analysis suggested also that swimmers tried to adjust their path when the linearity was lost and that this attempts took a lot of time to be carried out compared to the technical events of stroke and breathing. Therefore, data of the last spectral window (>2.5 s) were assigned to the event ‘voluntary adjustments’ (i.e. any attempt of the swimmer to go back to the ideal trajectory when it has lost). Multiple linear regression with enter method has been used to test the association among swimming speed and all three spectral windows above described. The enter method is a statistical tool that permits the simultaneous analysis of the dependence of the amplitude of all spectral windows on the swimming speed using all predictor variables, even if one of them - by itself - is not significantly associated with the dependent variable (Tabachnick and Fidell, 2001). According to the spectral windows chose, the following linear model has been used (equation 2):
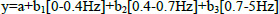 |
Equation 2 |
where y is the swimming speed, a is the intercept, and b1, b2, b3 are the unstandardized slopes (i.e. slopes that come from raw data) of the multiple linear regression. By using this model is possible to minimize the error of inferential estimation of the swimming speed and to evaluate the influence of the amplitude of each spectral window on overall swimming speed. In other words this model allows to estimate the overall swimming speed as a function of the amplitude of the spectral windows chose. Statistical analyses were performed with either a specific macro prepared with Visual Basic software (Microsoftr Excel) for the analysis, or by using SPSS (ver. 13.0) software package. The alpha level of significance was set at 0.05.
Average race times and the coefficient of variation are showed in Figure 2 for each length, not taking into account the underwater phases (i.e. 40 m of the Y-axis). The graph shows a high average swimming speed (m·s-1) in both the first one and the last 2 lengths. On the contrary, the average swimming speed of the middle race lengths is lower and shows a lowering trend. The coefficient of variation shows an increasing trend throughout the race. Figure 3 shows, for all swimmers and for each length, the linear relationship between mean forward speeds and mean LF speed-forward speed ratios, i.e. an “index” of speed wastage (see Discussion and Figure 3 caption for details). The intercept value obtained by the multiple linear regression model used was 1.752, which means an ideal average race time of 228.3 seconds (50 meters · 8 lengths / 1.752), i.e. 3 minutes, 48 seconds and 31 cents. Since the actual average time measured was 254.72 seconds, swimming along the perfect linear path would theoretically reduce the race time by about 10% [(254.72-228.3)/254.72*100]. The trends of the 3 spectral windows of LF obtained from DFT analysis are plotted against average swimming speeds of each length in Figure 4. Results show a clear increasing linear trend with the progressing of the race. In order to test the predictivity of spectral windows, multiple linear regression with enter method was performed. The amplitude of the spectral windows resulted significantly correlated with swimming speed (F = 5.23, d.f. = 3;91, p < 0.05). Two over three predictor variables were correlated with speed: voluntary adjustments (unstandardized slope = -0.58; p < 0.05) and strokes (unstandardized slope = -0.20; p < 0.05). Multiple determination coefficient was R2 = 0.147. Stroke (1.30 ± 0.11s) and breathing (1.84 ± 0.01s) period values confirmed the association with the relevant spectral windows. The contributions of the 3 spectral windows to the overall LF explain 14.7% of the variations of the average forward velocity during the race. Figure 5 shows the contribution (%) of the 3 spectral windows analyzed to the average energy wasting of each length. The contribution of each spectral window appears quite stable throughout the race; approximately, 55% may be attributed to strokes, 35% to voluntary adjustments, and only 10% to breathings. The aim of this study was to evaluate path linearity and some related variables of elite swimmers during a top-level competition of 400 m front crawl, in order to identify specific performance pattern. Race speeds of each 40 m length resulting from this study (Figure 2), without considering the underwater phases, are in line with average speeds found in literature (Laffite et al., 2004; Robertson at al., 2009), included the highest swimming speed of the first length, which is attributable to the dive start (Laffite et al., 2004). Average swimming speeds during the midsection of the race resulted lower than the first and the last 2 lengths. The speed increase in the last 2 lengths is probably due to both the higher exertion, given the approaching of the ending of the race, and the absence of the flip turn in the last length. The increasing trend of the coefficient of variation of speed highlights the heterogeneity, among swimmers, of fatigue accumulation with the progression of the race. This may be due to both intrinsic physiological (e.g. training status) and psychological (e.g. approach to the race) differences among athletes, and different strategies (e.g. strength saving) adopted. The forward speed and LF-forward speed ratio (Figure 3), which may represent an index of ‘speed wastage’, evidenced a linear relationship between the 2 variables. In other words, powerful upper arms strokes may generate high accelerations but, on the other hand, may also be the cause of wide LF, especially when the athlete gets fatigued. Di Prampero et al. (1974) also submitted this last hypothesis earlier, speculating that with fatigue swimmers may pay less attention to body alignment. Practically, the forward speed wastage in elite swimmers during high level 400 m front crawl competitions should ranges from 2.9 to 3.2 for the slower and faster race lengths, respectively (see Figure 3). Multiple regression analysis of DFT windows highlights the importance of the arm stroke technique in front crawl swim performance of elite athletes (Figure 4). The LFs were significantly and negatively correlated with the spectral window corresponding to the strokes (0.7-5 Hz). Probably, arm stroke modifies with the progression of the race and the progressive increase of fatigue. In fact, comparing the 0.7-5 Hz spectral windows amplitude of the 8 lengths, an increasing trend is detectable while progressing from 1st to 8th length (see Figure 4). This variation may be partly responsible for the speed reduction. Although the breathing window did not significantly correlate with forward speed, the trend was very similar to the arm stroke window. As a matter of fact, the breathing action is integrated into the stroke cycle (Payton at al., 1999; Sanders, 1995); thus one can speculate that the same discussion made for strokes may be made also for breathings. In line with the hypothesis discussed, from a practical standpoint training should not be solely focused on the improvement of aerobic, power and strength capacities related to the improvement of physical abilities, but also in refining stroke and breathing techniques in order to maintain the path linearity even when the swimmer get fatigued. Taken together the contributions of the 3 spectral windows to the overall LF explain 14.7% of the variations of the average forward velocity during the race. Although it is obviously not possible to remove completely LF because athletes cannot swim along a perfectly linear path, a reduction of the percentage of variations certainly leads to a better performance. In fact, the ideal race time of the swimmers could be estimated by means of the velocity resulting from multiple regressions. Obviously, this is just a raw estimation because it is affected by a random error that is mostly due to the localization, on the swimmer, of the reference point (the head). The body movements ineffective for the forward motion of the swimmer can be expected to lead to energy dissipation “per se”, and to require an additional effort to recover the correct position, with predictable negative consequences on performance. In terms of percentages, strokes, breathings, and voluntary adjustments contributed to LF, on average, by approximately 55%, 10%, and 35%, respectively (Figure 5). The data of the present study suggest that the LF included in the 0.4-5 Hz DFT range, due mostly to the technical events of arm stroke and breathing, may be reduced by training the proper technique in the pre-competition periods, with indubitable benefits on the performance. LF between 0-0.4 Hz may be the result of one or both the following: i) loss of path linearity mostly due to the accumulation of fatigue with the progressing of the race; ii) strategic choices taken autonomously by the swimmer during the race. In both cases, the voluntary adjustment needed to go back to the ideal trajectory are far more energy consuming than maintaining the path linearity. The analysis of an athlete body attitude during swim is very difficult to study, particularly during official competitions. Although photogrammetric techniques, with more cameras and focused on smaller acquisition field, may succeed in analyzing some detailed aspects of the swimming biomechanics (McCabe at al., 2011; Payton et al., 1999), their principal limitation is that they can only analyze few arm strokes. The present study analyzed the overall race but some limitations still exist in the accuracy and in the precision of the technique. Firstly, the acquisition technique was performed on a very wide space and secondly the whole head of each swimmer was used as reference point of his body. The development of acquisition technique based on inertial sensors placed on the athlete body (Davey et al., 2005) may rise the possibility to confirm and deepen the results here presented, although is very unlikely that this kind of devices will be ever permitted during an official competition. The results of this study may define a reference scheme for the study of the aspects of the swimming performance regarding path linearity of 400 m front crawl races. Specifically, strokes, voluntary adjustments, and breathings are key factors in this context. Thus, coaches and athletes, working on stroke technique for propulsion and on voluntary adjustments for strategy purpose, should also pay attention to the relevant influences on path linearity as a side effect. |
| AUTHOR BIOGRAPHY |
|
 |
Giorgio Gatta |
| Employment: Research fellow, University of Bologna |
| Degree: PhD |
| Research interests: Biomechanic and bioenergetic in swimming |
| E-mail: giorgio.gatta@unibo.it |
| |
 |
Matteo Cortesi |
| Employment: Teacher in Swimming Sport University of Bologna |
| Degree: PhD |
| Research interests: Biomechanic and bioenergetic in swimming |
| E-mail: m.cortesi@unibo.it |
| |
 |
Francesco Lucertini |
| Employment: Research Fellow, Department of Biomolecular Sciences, Division of Exercise and Health Sciences, of the University of Urbino Carlo Bo |
| Degree: PhD |
| Research interests: Exercise protocols, performance assessment, and biomechanics, in both health- and sport-related topics. |
| E-mail: francesco.lucertini@uniurb.it |
| |
 |
Benelli Piero |
| Employment: Medical Doctor, Sport Medicine Specialist |
| Degree: PhD |
| Research interests: Athelte's Assessment and Water exercise |
| E-mail: pierobenelli@alice.it |
| |
 |
Davide Sisti |
| Employment: University of Urbino Carlo Bo |
| Degree: PhD |
| Research interests: Biostatistic applications |
| E-mail: davide.sisti@uniurb.it |
| |
 |
Silvia Fantozzi |
| Employment: Research fellow at the University of Bologna |
| Degree: PhD |
| Research interests: Human movement analysis in orthopaedics and sports science applications |
| E-mail: silvia.fantozzi@unibo.it |
| |
|
| |
| REFERENCES |
 Aujouannet Y.A., Bonifazi M., Hintzy F., Vuillerme N., Rouard A.H. (2006) Effects of a high-intensity swim test on kinematic parameters in high-level athletes. Applied Physiology, Nutrition, and Metabolism 31, 150-158. |
 Canny J. (1986) A computational approach to edge detection. IEEE Trans, Pattern Anal: Machine Intell 8, 679-698. |
 Cappozzo A. (1984) Gait analysis methodology. Human Movement Science 3, 27-54. |
 Clarys J.P., Terauds J., Bedingfield E.W. (1979) Swimming III. Human morphology and hydrodynamics. Baltimore. University Park Press. |
 Colwin M.C. (2002) . Breakthrough swimming. London. Pelham Books. |
 Craig A.B., Skehan P.L., Pawelczyk J.A., Boomer W.L. (1985) Velocity, stroke rate, and distance per stroke during elite swimming competition. Medicine and Science in Sports and Exercise 17, 625-634. |
 Davey N., Anderson M.E., James DA. (2005) An accelerometer-based system for elite swimming performance analysis. Proceedings of SPIE the International Society for Optical Engineering 5, 409-415. |
 Di Michele R., Gatta G., Leo A.D., Cortesi M., Andina F., Tam E., Boit M.D., Merni F. (2011) Estimation of the anaerobic threshold from heart rate variability in anincremental swimming test. The Journal of Strength and Conditioning Research 26, 3059-3066. |
 di Prampero P.E., Pendergast D.R., Wilson D.W., Rennie DW. (1974) Energetics of swimming man. Journal of Applied Physiology 37, 1-4. |
 Gatta G., Ditroilo M., Sisti D., Cortesi M., Benelli P., Bonifazi M. (2008) The assessment of path linearity in swimming: a pilot study. International Journal of Sports Medicine 29, 959-964. |
 Gatta G., Zamparo P., Cortesi M. (2013) Effect of swim cap model on passive drag. The Journal of Strength and Conditioning Research 27, 2904-2908. |
 Laffite L.P., Vilas-Boas J.P., Demarle A., Silva J., Fernandes R., Billat V.L. (2004) Changes in physiological and stroke parameters during a maximal 400-m free swimming. Canadian Journal of Applied Physiology 29, 17-31. |
 Maglischo E.W. (2003) . Swimming Fastest. Champaign. Human Kinetics. |
 McCabe C.B., Psycharakis S.G., Sanders R.H. (2011) Kinematic differences between front crawl sprint and distance swimmers at sprint race. Journal of Sports Sciences 29, 115-123. |
 Payton C.J., Bartlett R.M., Baltzopoulos V., Coombs R. (1999) Upper extremity kinematics and body roll during preferred-side breathing and breath-holding front crawl swimming. Journal of Sports Sciences 17, 689-696. |
 Pocock S.J. (1974) Harmonic Analysis Applied to Seasonal Variations in Sickness Absence. Journal of the Royal Statistical Society 23, 103-120. |
 Robertson E., Pyne D., Hopkins D., Anson J. (2009) Analysis of lap time in international swimming competitions. Journal of Sports Sciences 27, 387-395. |
 Sanders R.H. (1995) Can skilled performers readily change technique? An example, conventional to wave action breaststroke. Human Movement Science 14, 665-679. |
 Seifert L., Chollet D., Brady B.G. (2004) Effect of swimming velocity on arm coordination in the front crawl: a dynamic analysis. Journal of Sports Sciences 22, 651-660. |
 Tabachnick B. G., Fidell L. S. (2001) . Using multivariate statistics. Boston, MA. Allyn and Bacon. |
 Toussaint H.M., Hollander A.P. (1994) Energetics of competitive swimming. Implications for training programmes. Sports Medicine 18, 384-405. |
 Vorontsov A.R., Rumyantsev V.A., Knuttgen H.G., Dirix A., Renstrom P.K., Tittel K. (2000) The Encyclopaedia of Sports Medicine An IOC Medical Commission Publication, Biomechanics in Sport: Performance Enhancement and Injury Prevention. Propulsive forces in swimming and resistive forces in swimming. London:. Blackwell Publishing. |
 Yanai T. (2003) Stroke frequency in front crawl: its mechanical link to the fluid forces required in non-propulsive directions. Journal of Biomechanics 36, 53-62. |
 Zamparo P., Gatta G., di Prampero P.E. (2012) The determinants of performance in master swimmers: an analysis of master world record. European Journal of Applied Physiology 112, 3511-3518. |
|
| |
|
|
|
|

