|
|
|
| |
| ABSTRACT |
|
Due to the difficulty of measuring forces and torques acting on a swimmer during mid-pool swimming, an inverse dynamics approach is required. Personalised body segment parameter (BSP) data enabling calculation of net forces and torques can be obtained using the elliptical zone method. The purpose of this study was to establish the reliability of estimating BSP data of swimmers by the elliptical zone method with segment outlines being traced manually on a personal computer screen. Five assessors digitised the segment landmarks and traced the body segments from front and side view digital photographs of 11 single arm amputee swimmers. Each swimmer was assessed five times by each of the five assessors. The order was fully randomised. Within assessor variability was less than 5% for the segment centre of mass position of all segments, for segment length except the neck (5.2%), and for segment mass except neck (11.9%), hands (Left: 8.1%; Right: 5.8%) and feet (Left: 7.3%; Right: 7.3%). Analysis of mean variability within and between assessors indicated that between assessor variability was generally as large or larger than within assessor variability. Consequently it is recommended that when seeking personalised BSP data to maximise the accuracy of derived kinetics and sensitivity for longitudinal and bilateral within-subject comparisons the individual should be assessed by the same assessor with mean values obtained from five repeat digitisations. This study established that using the elliptical zone method using E-Zone software is a reliable and convenient way of obtaining personalised BSP data for use in analysis of swimming. |
| Key words:
Anthropometry, elliptical zone, error, inverse dynamics, reliability, Paralympic, swimming
|
Key
Points
- A unique (not been attempted previously) study of reliability of calculating personalised Body Segment Parameter (BSP) data using the elliptical zone method
- Establishes benchmark data regarding the reliability of BSP data for comparison with emerging technologies for obtaining personalised BSP data non-invasively.
- Provides a description and guidelines for good practice for maximising the accuracy of derived kinematics and kinetics in swimming.
- The method of body modelling described can also be applied to studies in other sports and in assessing change in health status related to body shape characteristics for sport and non-sport populations.
|
Obtaining accurate body segment parameter (BSP) data such as segment masses, segment centre of mass positions and moments of inertia is fundamental to calculating the kinematics and kinetics of human motion from anatomical reference points digitised from video. While personalised BSP data may be useful in the analysis of any human motion, it is particularly important in analysis of mid-pool swimming where direct measurement of kinetics is extremely difficult. Net force, the product of the second derivative of whole body centre of mass (COM) position and body mass, can indicate the instantaneous balance between propulsive and resistive forces, thereby enabling an assessment of the effectiveness of technique and the relative contributions by the right and left limbs. Direct measurement of swimming speed has been used to gather this information by attaching a light line to a fixed point on the swimmer’s body, commonly the hips (e.g. Payton and Wilcox, 2006). However, the speeds and derived accelerations based on the motion of the hips have been shown to differ considerably from the motion of the COM (Figueiredo et al., 2009; Psycharakis and Sanders, 2009). With respect to angular motion, the inverse dynamics approach of Dapena (1978) has been applied to swimming to estimate net torques about the longitudinal axis (body roll) (Yanai, 2004), the transverse axis (pitch) (Yanai, 2001) and about the vertical axis (yaw) (Sanders and McCabe, 2014). The patterns of roll (Yanai, 2004) and yaw (Sanders and McCabe, 2014) have been found to be linked to technique asymmetries and to swimming performance. In addition to understanding and assessing technique of able bodied swimmers, quantification of linear and angular kinetics are necessary to explore the effects of disabilities on performance and to shed light on the issue of classification in Paralympic swimming. In many cases, the disabilities create morphological asymmetries which affect the balance of torques acting during swimming, for example, the effect of missing limbs on the roll and pitch of the body in response to bilateral asymmetries in the torques due to gravity and buoyancy. Thus, input of personalised segment BSP data is essential to obtain realistic results. Additionally, change in the anthropometric data themselves is of interest when assessing the effect of body mass, and its distribution, on swimming performance. For this reason it is important to establish the sensitivity of the BSP measurements and the confidence with which changes over time can be detected. Several methods have been developed for estimating BSP data. These include using data based on cadavers (Depster, 1955; Dempster and Gaughran, 1967; Clauser et al., 1969), dual energy X-ray absorptiometry (Durkin et al., 2002), magnetic resonance imaging (Martin et. al., 1989; Pearsall et al., 1994), computer tomography (Pearsall et al.,), gamma ray scanning (Casper et al., 1971), surface 3D scanning combined with computer aid design (Ma et al., 2011). One method of obtaining personalised estimates of these parameters inexpensively and non-invasively is by modelling segments as a series of ellipses of known depth and diameters (Jensen, 1978). The volume of each ellipse is then determined and, in conjunction with estimates of density, the mass of each ellipse can be found. The position of the centre of mass of the segment relative to a meaningful landmark or segment endpoint can then be determined by summing moments about the three anatomical axes of the segment. The moments of inertia about each of the anatomical axes of each segment can be determined by summing the local and remote terms of the contributions of each ellipse by applying the parallel axis theorem (Hay, 1993). The diameters of the ellipses are obtained by tracing the outline of the segments from two photographs taken from orthogonal perspectives. The reliability of the measurements depends on the consistency of tracing those outlines as well as digitising the anatomical landmarks that define each body segment. Reliability of the method is particularly important when the body segment parameter data are used in longitudinal studies in which changes in body morphology and mass distribution are likely. Sanders (1991) showed that forces derived from COM data based on BSP data obtained using the elliptical zone method matched the actual forces measured by a force plate in a drop jumping task with the exception of the high frequency contributions associated with impact. Therefore, it could be expected that the method could be applied well to mid-pool swimming where forces are comprised of low frequency contributions. Reliability of the elliptical zone method has been maximised in the past by projecting slides onto large digitising tablets (Jensen and Fletcher, 1994; Tupling et al., 1984). Tupling et al. (1984) indicated that the adapted elliptical zone method is consistent in day-to-day measuring or by different assessors. Therefore, the past elliptical zone methods have been applied in longitudinal studies to determine the variation of humans’ body shape, volume, mass, radius, and moments of inertia of segments (Jensen and Nassas, 1985; Jensen 1986a; 1986b; 1987; 1989; Yokoi et al., 1986). With the advancement in software, enabling user interaction with digital photographs, digitising and tracing of body segments can be achieved readily on personal computers. A MATLAB program (E-Zone) enabling the acquisition of the ellipse diameters and subsequent calculation of body segment parameter data using the elliptical zone method has been developed (Deffeyes and Sanders, 2005). Figure 1 shows some graphical output of the MATLAB program with the body modelled as ellipses. Table 1 indicates that E-Zone is the only BSP data collection method that meets all the criteria relating to accuracy, cost, portability, accessibility, speed, and being free of health risks. More body dimensions (segment breadths and depths) are used by E-Zone than other mathematical models so more accurate BSP data can be obtained for biomechanical analysis. E-zone requires only two digital cameras allowing easy availability, low cost, and portability compared with photonic or medical scanners. Digitising and calculations of a subject can be completed within 20 minutes. To date, there is a paucity of data regarding the reliability of the measurements obtained both in terms of within assessor variability and between assessor variability. One of the very few papers to report reliability of these methods was a study of front crawl swimmers by Psycharakis et al. (2010) in which within-operator standard deviation of total body mass was reported as 0.4kg and the coefficient of variation as 0.3%. The purpose of the current study was to establish the reliability of body segment parameter data obtained using the elliptical zone method with segment endpoints and outlines being digitised and traced manually on a personal computer screen using E-Zone. The contribution to variability of differences between assessors trained in digitising and tracing the body segments, and the contribution to variability of differences within assessors between repeated digitisations and tracings, were evaluated. For application to analysis of both able bodied and Paralympic swimming, establishing the sensitivity of measurement was of particular interest. In future studies of swimming this will inform the confidence with which the effect of bilateral differences on torsional balance, and the effect on performance of longitudinal changes in morphology with exercise and diet, can be assessed. ParticipantsParticipants in this study comprised 11 single arm amputee swimmers (9 females, 2 males) whose body segment parameter data were required for subsequent video based three-dimensional (3D) analysis of swimming technique. The mass of the nine female single arm amputee swimmers ranged from 44.8 kg to 67.4 kg while the masses of the two male single arm amputee swimmers were 99.1 kg and 71.6 kg (Table 2). Heights ranged from 1.57m to 1.67m (females) and 1.84m to 1.86m for the two males (Table 2). Swimmers wore nylon competition swimming suits (not body suits) so that all segment endpoint landmarks could be palpated and marked as described by Deffeyes and Sanders (2005).
AssessorsFive assessors digitised and traced the segment outlines from digital photographs of the swimmers. The assessors underwent training to gain familiarity with the MATLAB program ‘E-Zone’ (Deffeyes and Sanders, 2005) used for digitising/tracing of the body segments and subsequent output of body segment parameter data applying the modelling methods of Jensen (1978). The training, conducted by the first author, comprised a demonstration and explanation of the elliptical zone method and the digitising/tracing techniques required to obtain accurate and reliable results. The most experienced assessor supervised three practice trials of the other assessors ensuring that the digitising and tracing protocols were applied consistently according to the original developers of this method (Jensen, 1978) and the developers of the E-Zone MATLAB program (Deffeyes and Sanders, 2005). Moreover training was utilised to assess the accuracy of each trial by comparing the participant’s actual total body mass (weighing scales) to the calculated total body mass (E-Zone output).
ProtocolSwimmers were weighed on a set of Seca 712 column scales (Germany) and their height measured (without shoes) on a Seca 225 stadiometer (Germany) ensuring that the spine at lumbar, thoracic and cervical regions was comfortably extended to achieve good natural postural alignment. Segment endpoints and landmarks (Table 3), on both sides of the body, were identified visually, palpated, and marked with black waterproof oil and wax based cream (Grimas Crème Make Up) which was applied with a 30 mm diameter circular sponge to the skin of the swimmer. In the case of the female swimmers, 30 mm black tape markers were adhered to the swim suit at the xiphoid process of the sternum and in-line laterally with this marker on the trunk, defining the border between the upper and lower trunk. For marking the vertex of the head, swimmers were required to wear a white silicon cap with a black marker applied at the highest point. The upper limbs on the affected side were marked at the elbow, if present, and the most distal endpoint. Participants adopted an erect posture with the lumbar, thoracic and cervical spine comfortably extended as described for the height measurement. The chin was elevated sufficiently to ensure that the line from mandible to chin was horizontal. Participants stood on an inclined board so that the feet were sloped at approximately 45 degrees to the horizontal enabling subsequent modelling of the feet as a stack of ellipses. The extended upper limbs were maintained predominantly in the mid-frontal plane with the palms facing forward, fingers adducted and thumb in the neutral position. The upper limbs were positioned sufficiently posteriorly that they did not obscure the hip marker from the side view and sufficiently anteriorly to also avoid obscuring the lumbar region (outline of the swimmer’s back) from the side view. Still photographs were taken simultaneously, using a ‘one, two, three, go’ command, by three digital cameras (Canon PowerShot S1 IS, Sony DSC-V1 and Sony DSC-T5) from front, left side, and right side views (Figure 2). All cameras had a 4.0 megapixel capacity. Photographs of each swimmer and the horizontal and vertical scales were taken separately without altering camera distances, focal lengths, or settings between photographs. The cameras were set on tripods at a height of 1m and their axes parallel to the horizontal floor surface and at a distance of 10m from where the swimmer would be positioned in order to minimise perspective errors and scaling errors due to the body surfaces being slightly out of the planes in which the linear scales were photographed. The cameras were zoomed to ‘3X’ magnification to maximise the image size for both the swimmer and the scale.
Data ProcessingEach of the assessors scaled, digitised, and traced each swimmer in a randomised order. The computer screens had a diagonal length of 27.5cm and a resolution of 1280 x 1024 pixels. The E-Zone software (Deffeyes and Sanders, 2005) enabled each body segment to be zoomed in turn to maximise the screen thus increasing the reliability of tracing. After completing the digitisation of all eleven swimmers, assessors then repeated that process, again in a randomised order, until each swimmer had been completed five times by each of the five assessors. To mimic likely real clinical scenarios in which repeat measures are taken with considerable temporal separation, no swimmer was assessed more than once on the same day by the same assessor. The body segment parameter (BSP) data output from E-Zone included segment volumes, segment masses, segment lengths, segment centre of mass position as a percentage distance between the landmarks, and moment of inertia about the segment medio-lateral (IML), antero-posterior (IAP), and longitudinal/proximal-distal (IPD) axes of the segments. The segments were head, neck, upper trunk, lower trunk, right and left arm, forearm, hand, thigh, shank, and foot. Values were also obtained for combined head and neck and combined thorax and abdomen.
Data analysisFour procedures were conducted to determine mean within assessor variability for each BSP for each body segment;Mean within assessor standard error of the true mean of five digitisations by an individual assessor of each BSP for each body segment; Between assessor variability due to the combined effect of differences in digitising and tracing technique among individuals;The change required between testing occasions in a longitudinal study, using a protocol of five digitisations per testing occasion, to be 95% certain that a real change has occurred.
1.To determine within assessor variability, means and standard deviations (SD) of the five trials of each swimmer were determined for each assessor for each of the BSP variables yielding 55 means and SDs for each BSP of each body segment. The standard deviations were expressed as coefficients of variation (SD/Mean×100) to take into account the magnitude of the measurement. The mean of the SDs and of the coefficients of variation (CV) across the assessors was obtained for each swimmer. The means of these across the 11 swimmers were then determined.
2.For each BSP variable of each body segment the standard error of the mean (SD/√n) of the five digitised trials was determined and expressed as a coefficient of variation of the mean (CVM) calculated as 100×SD/(√5 × Mean). This provided an indication of the reliability of the measurement when a protocol of five repeated digitisations is used and the mean taken as the representative value. This protocol may be adopted in practice where precise measures are required.
3.Means of the five digitisations of each of the five assessors were obtained for each of the 11 swimmers (55 means) for each BSP variable and body segment. Then the SDs and CVs across the five means for each swimmer were obtained as measures of variability between assessors. Means of those SDs and CVs across the 11 swimmers were then obtained as overall estimates of between assessor variability. Given that the total variability between assessors contains some variability due to the errors in the mean of the five digitised trials of the individual assessors, in addition to the systematic variability due to differences in digitising and tracing technique, these were then assessed in conjunction with the standard error of the mean and the corresponding coefficients of variation of the mean.
4.For each variable, an independent t-test was applied to determine the smallest change required, expressed as a percentage, to be 95% certain that a change had occurred in tests conducted by the same assessor on an individual longitudinally using a five digitisation per sample protocol. The test is independent because the five digitisations taken on each occasion are not correlated according to their order. The formula (Hinton, 2004) is given as:
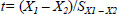 |
Eq 1 |
Where X1 and X2 are the means of the variable for the five digitisations of the first testing occasion and second testing occasion respectively and SX1 – X2 is the estimated standard error. When the number of digitisations is equal on each testing occasion the formula to estimate the standard error is:
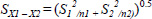
Where S1 and S2 are the standard deviations of the digitisations of each sample and n is the number of samples. In this case, the standard deviation on successive occasions is the mean within assessor SD determined as described in 1. Given that n is 5, the formula for the standard error simplifies to:
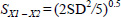
Substituting into the original equation (Eq 1), the formula for t becomes:
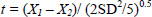 |
Eq 2 |
Working with coefficients of variation to normalise to percentages of the means as described in 1, and rearranging to determine the difference required to reach 95% confidence that there has been a change, we have
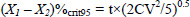
Where (X1 – X2)%crit95 is the change required to be confident of an actual change at the 95% level of confidence.
In looking at the effects of a nutritional or exercise intervention we would expect a change in a particular direction and hence apply a one tailed test and the value of t with n-1(4) degrees of freedom the t value is 2.132. While the overall means for the measures of variability described above were determined across 11 swimmers, exceptions were the hands and forearms due to the amputations. In the case of the left forearm and hand, means were obtained from the four swimmers whose left forearms and hands were intact and in the case of the right forearms and hands, means were obtained from the seven swimmers whose right forearms and hands were intact. Despite some arms being short due to partial amputation, the mean variability in measures of the right and left arms was obtained from all swimmers regardless of whether the limbs were complete or partial. This did not affect the measures of variability given that the measures of variability were within and between assessors rather than between swimmers.
Within assessor reliabilityMean within-assessor SD, CV, and CVM (results of procedures 1 and 2) for the BSP data of each segment are presented in Table 4. It is apparent that CVs are smaller for the large segments than the small segments, for example 1.3% for the mass of the abdomen compared to 8.1% for the mass of the left hand. CVs for moments of inertia were large compared to the CVs for other variables, for example, 2.5% for the IML of the abdomen and 11.7 for IML of the left hand.
Between assessor reliabilityMean between assessor SD and CV for BSP data of each segment (results of procedure 3) are presented in Table 5. Between assessor reliability was of a similar magnitude to within assessor reliability and in many cases somewhat larger, for example between assessor reliability for the mass of the abdomen was 1.5% compared to 1.3% for within assessor reliability and 3.9% compared to 2.5% for IML.
Change required for 95% confidenceMean within-assessor CV and change required to have 95% confidence of a real difference in longitudinally sampled means using a within assessor protocol with five digitisations on each testing occasion (results of procedure 4) are presented in Table 6. Of particular interest with respect to monitoring changes in body shape of swimmers is the sensitivity to detecting changes in mass of the large segments. Assessors can be confident of a real change when measures on separate occasions exceed 1.8% for the abdomen, 2.3% for the thorax, and 2.7% for the thighs. Changes in the combined thorax and abdomen can be detected confidently with only a 1.3% change.
The purpose of this study was to establish the reliability of body segment parameter data obtained using the elliptical zone method with segment endpoints and outlines being digitised and traced manually on a personal computer screen using E-Zone software. An error margin of 5% has been used as a useful criterion for reporting overall reliability in accordance with convention. Within assessor variability indicated by CV for the COM position as a percentage of the distance from proximal to distal joint centres was less than 5% for all body segments. Within assessor variability of segment mass was also less than 5% for all body segments except neck (11.9%), hands (Left:8.1%; Right:5.8%) and feet (Left:7.3%; Right:7.3%). Variability in length was less than 5% for all segments except the neck (5.2%). In the case of the neck the SD was smaller than many of the other segments but the CV was larger due to the segment’s relatively short length. Variability in moments of inertia was larger than the other BSPs. This was due to the calculation being the sum of the local inertia terms of the ellipses and the remote terms. The remote terms in particular are sensitive to error, being the product of mass and squared radii of the ellipse centres of mass from the whole segment centre of mass. Consequently, variability in each of the terms has a compounding effect on the variability of the calculated moment of inertia. Nevertheless CVs were below 5% for the large body segments that have the greatest effect on torque and angular momentum determined from position data. Variability was larger for the small segments in terms of CVs but was small in terms of the magnitude of the variability expressed as an SD. For example the SDs of the IAP and IML moments of inertia of the hands were less than 1/100th of those of the abdomen but the CVs were more than three times those of the abdomen. The between assessor variability data shown in Table 5 reflect systematic differences in digitising and tracing techniques among the assessors and also includes some random error due to within assessor variability. However, the latter is less than the within assessor errors due to the means of five digitisations being used to assess differences between assessors. A conservative estimate of the effect of the within assessor contribution to between assessor error is therefore the CVMs presented in Table 4. Taking the within assessor contribution into account, the magnitude of the systematic error contribution to total variability among assessors is generally similar to or greater than that of the within assessor variability. Given that differences between assessors tend to be similar to or greater than the within assessor variability it is recommended that, when using E-Zone to monitor changes in anthropometric variables, a protocol should be adopted whereby individuals undergoing repeated longitudinal examinations are assessed by the same assessor. To increase confidence in detecting changes in anthropometric characteristics of individuals, means of multiple digitisations can be obtained and compared across testing occasions. When using a single assessor protocol with five repeated digitisations on each testing occasion, the magnitudes of changes required to be 95% confident that there is a definite change (i.e. for the change to be statistically significant at p < 0.05) are presented in Table 6. Of greatest relevance are the changes in mass of the body segments estimated from changes in volume. Thus, if a change of 1.5% in the mass of the combined thorax and abdomen was found we would be confident of a ‘real’ change between two testing occasions. The change required to detect changes with 95% confidence naturally increases with decreasing size of the segment. For example differences in means of 6% between testing occasions are required to be confident of a real change in mass of the arms. However, the thighs, another area of the body that is likely to change mass through exercise or dietary interventions, requires only a 2.5% difference in means to be confident of a real change. Given the advantages of the elliptical zone method compared to other methods discussed in the introduction and shown in Table 1, using E-Zone to obtain personalised BSP data would appear to be a good choice at this time given that the results of this study show that reliability is generally good. The method of body modelling described can also be applied to studies in other sports and in assessing change in health status related to body shape characteristics for sport and non-sport populations. New technologies are enabling further development of volumetric BSP modelling techniques but have not yet been refined and tested sufficiently. These include automatic edge detection to replace manual tracing. However, these methods are subject to variability due to factors such as camera placement, lighting/shadow, contrast conditions due to skin/clothing colour and background. The reliability of the E-Zone method involving manual tracing will provide a benchmark against which the emerging methods can be compared and validated. The elliptical zone method with E-Zone software can be used as a non-invasive and portable method of assessing body segment characteristics. To optimise the reliability of interpreting results, particularly when assessing changes of individuals longitudinally, or when the effect of bilateral asymmetries is being investigated, the same assessor should assess the individual on each testing occasion and means of several digitisations should be used. Conflict of interestThe authors declare that there is no conflict of interest with regard to this paper for any author.
|
| AUTHOR BIOGRAPHY |
|
 |
Ross H. Sanders |
| Employment: Professor and Head of Exercise and Sport Science at The University of Sydney in the Faculty of Health Sciences |
| Degree: PhD |
| Research interests: Bridge biomechanics and motor control and learning with specific emphasis on movement asymmetries and rhythms. |
| E-mail: ross.sanders@sydney.edu.au |
| |
 |
Chuang-Yuan Chiu |
| Employment: Centre for Aquatics Research and Education (CARE), The University of Edinburgh. |
| Degree: PhD student |
| Research interests: Anthropometric modelling of the human body |
| E-mail: thorsten.chiu@gmail.com |
| |
 |
Tomohiro Gonjo |
| Employment: Centre for Aquatics Research and Education (CARE), The University of Edinburgh. |
| Degree: PhD student |
| Research interests: Biophysical research of front crawl and back crawl in swimming |
| E-mail: T.Gonjo@sms.ed.ac.uk |
| |
 |
Jacki Thow |
| Employment: PhD student, Edinburgh University |
| Degree: BSc, MSc |
| Research interests: Applied biomechanical analysis of swimming and coaching science |
| E-mail: Jacki.thow@googlemail.com |
| |
 |
Nuno Oliveira |
| Employment: Centre for Aquatics Research and Education, University of Edinburgh |
| Degree: PhD |
| Research interests: Biomechanics and motor control of human performance |
| E-mail: nunocancela@gmail.com |
| |
 |
Stelios G. Psycharakis |
| Employment: The University of Edinburgh |
| Degree: PhD |
| Research interests: Biomechanics research on human performance, with a growing emphasis on clinical applications. |
| E-mail: Stelios.Psycharakis@ed.ac.uk |
| |
 |
Carl J. Payton |
| Employment: Reader in Biomechanics in the Department of Exercise and Sport Science at Manchester Metropolitan University |
| Degree: PhD |
| Research interests: sports performance, with a particular focus on the biomechanics of elite swimmers, including those with a disability. |
| E-mail: c.payton@mmu.ac.uk |
| |
 |
Carla B. McCabe |
| Employment: Ulster Sports Academy, University of Ulster |
| Degree: PhD |
| Research interests: Biomechanical analysis of swimming and aquatic exercise |
| E-mail: c.mccabe@ulster.ac.uk |
| |
|
| |
| REFERENCES |
 Casper R.M., Jacobs A.M., Kenney E.S., McMaster I.B. (1971) On the use of gamma ray images for the determination of human body segment mass parameters. Proc. SPIE 0026, Quantitative Imagery in the Biomedical Sciences I , 49-. |
 Clauser C.E., McConville J.T., Young J.W. (1969) AMRL Tech. Report 69-70. Weight, volume, and center of mass of segments of the human body. Dayton, OH. Wright Patterson Air Force Base. |
 Damavandi M., Farahpour N., Allard P. (2009) Determination of body segment masses and centers of mass using a force plate method in individuals of different morphology. Medical Engineering and Physics 31, 1187-1194. |
 Dapena J. (1978) A method to determine the angular momentum of a human body about three orthogonal axes passing through its center of gravity. Journal of Biomechanics 11, 251-256. |
 Deffeyes J., Sanders R.H., Wang Q. (2005) Proceedings of XXIII International Symposium on Biomechanics in Sports. Elliptical zone body segment modelling software: digitising, modelling and body segment parameter calculation. Beijing. The China Institute of Sports Science. |
 Dempster W.T. (1955) . Space Requirements of the Seated Operator: (WADC TR-55-159). Dayton, OH. Wright-Patterson Air Force Base. |
 Dempster W.T., Gaughran G.R.L. (1967) Properties of body segments based on size and weight. Amercian Journal of Anatomy 120, 33-54. |
 Durkin J.L., Dowling J.J., Andrews D.M. (2002) The measurement of body segment inertial parameters using dual energy x-ray absorptiometry. Journal of Biomechanics 35, 1575-1580. |
 Figueiredo P., Vilas Boas J.P., Maia J., Gonçalves P., Fernandes R.J. (2009) Does the hip reflect the centre of mass swimming kinematics?. International Journal of Sports Medicine 30, 779-781. |
 Hay J.G. (1993) . The Biomechanics of Sports Techniques. Englewood Cliff, NJ. Prentice Hall. |
 Hinton P.R. (2004) . Statistics Explained. London. Routledge. |
 Jensen R.K. (1978) Estimation of the biomechanical properties of three body types using a photogrammetric method. Journal of Biomechanics 11, 349-358. |
 Jensen R.K. (1986a) Body segment mass, radius and radius of gyration proportions of children. Journal of Biomechanics 19, 368-. |
 Jensen R.K. (1986b) The growth of children’s moment of inertia. Medicine and Science in Sports and Exercise 18, 1-5. |
 Jensen R.K. (1987) Growth of estimated segment mass between four and sixteen years. Human Biology 59, 173-189. |
 Jensen R.K. (1989) Changes in segment inertia proportions between 4 and 20 years. Journal of Biomechanics 22, 529-536. |
 Jensen R.K., Fletcher P (1994) Distribution of mass to the segments of elderly males and females. Journal of Biomechanics 27, 89-96. |
 Jensen R.K., Nassas G., Coblentz A.M., Herron R.E. (1985) Biosteriometrics ‘85’ SPIE. A mixed longitudinal description of body shape growth. Bellingham, WA. |
 Lee C., Sanders R.H., Payton C. (2014) Changes in force production and stroke parameters of trained able-bodied and unilateral arm amputee female swimmers during a 30 s tethered front crawl swim. Journal of Sports Sciences 32, 1704-1711. |
 Ma Y., Kwon Y., Zhihong M., Lee K., Li L., Chung H. (2011) Segment inertial parameters of Korean adults estimated from three-dimensional body laser scan data. International Journal of Industrial Ergonomics 41, 19-29. |
 Martin P.E., Mungiole M., Marzke M.W., Longhill J.M. (1989) The use of magnetic resonance imaging for measuring segment inertial properties. Journal of Biomechanics 22, 367-376. |
 Payton C., Baltzopoulos V., Bartlett R. (2002) Contributions of rotations of the trunk and upper extremity to hand velocity during front crawl swimming. Journal of Applied Biomechanics 18, 243-256. |
 Payton C., Sanders R.H., Seifert L., Chollet D., Mujika I. (2011) World Book of Swimming: From Science to Performance. Body roll in front crawl swimming. Nova Science Publishers. |
 Payton C.J., Bartlett R.M., Baltzopoulos V., Coombs R. (1999) Upper extremity kinematics and body roll during preferred-side breathing and breath-holding front crawl swimming. Journal of Sports Sciences 17, 689-696. |
 Payton C.J., Hay J.G., Mullineaux D.R. (1997) The effect of body roll on hand speed and hand path in front crawl swimming-A simulation study. Journal of Applied Biomechanics 13, 300-315. |
 Payton C.J., Wilcox C. (2006) Intra-cyclic speed fluctuations of uni-lateral arm amputee front crawl swimmers. Portuguese Journal of Sport Sciences 6, 73-75. |
 Pearsall D., Reid J., Ross R. (1994) Inertial properties of the human trunk of males determined from magnetic resonance imaging. Annals of biomedical engineering 22, 692-706. |
 Pearsall D.J., Reid J.G., Livingston L.A. (1996) Segmental inertial parameters of the human trunk as determined from computed tomography. Annals of Biomedical Engineering 24, 198-210. |
 Psycharakis S., Sanders R.H. (2008) Shoulder and hip roll changes during 200-m front-crawl swimming. Medicine and Science in Sports and Exercise 40, 2129-2136. |
 Psycharakis S., Sanders R.H. (2009) Validity of the use of a fixed point for intracycle velocity calculations in swimming. Journal of Science and Medicine in Sport 12, 262-265. |
 Psycharakis S.G., McCabe C.B. (2011) Shoulder and hip roll differences between breathing and non-breathing conditions in front crawl swimming. Journal of Biomechanics 44, 1752-1756. |
 Psycharakis S.G., Sanders R., Mill F., Wang Q. (2005) Proceedings of XXIII International Symposium on Biomechanics in Sports. A Calibration Frame for 3D Swimming Analysis. Beijing. The China Institute of Sports Science. |
 Psycharakis S.G., Sanders R.H. (2010) Body roll in swimming: A review. Journal of Sports Sciences 28, 229-236. |
 Sanders R. H., Wilson B. D., Jensen R. K. (1991) Accuracy of derived ground reaction force curves for a rigid link human-body model. International Journal of Sport Biomechanics 7, 330-343. |
 Sanders R., McCabe C., Mason B (2014) Handbook of the 12 International Symposium on Biomechanics and Medicine in Swimming. Asymmetries produce yaw in breaststroke. Canberra ACT. Australian Institute of Sport. |
 Sanders R.H., Psycharakis S.G. (2009) Rolling rhythms in front crawl swimming with six-beat kick. Journal of Biomechanics 42, 273-279. |
 Tupling S.J., Pierrynowski M.R., Forsyth R.D., Thornton-Trumm A.B. (1984) Human Locomotion 111. Anthropometric estimates of the human body using photogrammetry. Winnipeg, Manitoba. Canadian Society for Biomechanics. |
 Yanai T. (2001) Rotational effect of buoyancy in frontcrawl: does it really cause the legs to sink?. Journal of Biomechanics 34, 235-243. |
 Yanai T. (2004) Buoyancy is the primary source of generating body roll in front crawl swimming. Journal of Biomechanics 37, 605-612. |
 Yokoi T., Shibukawa K., Ae M. (1986) Body segment parameters of Japanese children. Japanese Journal of Physical Education 31, 53-. |
|
| |
|
|
|
|

