|
|
|
| |
| ABSTRACT |
|
This study investigated the effect of projection angle on the distance attained in a rugby place kick. A male rugby player performed 49 maximum-effort kicks using projection angles of between 20 and 50°. The kicks were recorded by a video camera at 50 Hz and a 2 D biomechanical analysis was conducted to obtain measures of the projection velocity and projection angle of the ball. The player’s optimum projection angle was calculated by substituting a mathematical expression for the relationship between projection velocity and projection angle into the equations for the aerodynamic flight of a rugby ball. We found that the player’s calculated optimum projection angle (30.6°, 95% confidence limits ± 1.9°) was in close agreement with his preferred projection angle (mean value 30.8°, 95% confidence limits ± 2.1°). The player’s calculated optimum projection angle was also similar to projection angles previously reported for skilled rugby players. The optimum projection angle in a rugby place kick is considerably less than 45° because the projection velocity that a player can produce decreases substantially as projection angle is increased. Aerodynamic forces and the requirement to clear the crossbar have little effect on the optimum projection angle. |
| Key words:
Biomechanics, kinematics, projectile
|
Key
Points
- The optimum projection angle in a rugby place kick is about 30°.
- The optimum projection angle is considerably less than 45° because the projection velocity that a player can produce decreases substantially as projection angle is increased.
- Aerodynamic forces and the requirement to clear the crossbar have little effect on the optimum projection angle.
|
The place kick is an important skill in rugby union as it can contribute to the team’s score through a penalty kick at goal (3 points) and through converting a try (2 points). A player who can produce a longer kick distance is able to attempt a penalty kick or try conversion from a greater fraction of the field of play and hence has a greater opportunity to score. The kick distance in a rugby place kick is determined mainly by the projection velocity and projection angle of the ball. It is well known that a higher projection velocity produces a longer kick distance and that players with greater muscular strength can produce a higher ball projection velocity (Cabri et al., 1988). Video analysis has shown that top-level rugby union players use a projection angle of around 30° (Holmes et al., 2006). However, the biomechanical rationale for this projection angle is not clear. The optimum projection angle for achieving the greatest distance in a rugby place kick is not expected to be 45°. Previous studies of throwing, jumping, and kicking events have shown that projection velocity and projection angle can be inter-related (Hubbard et al., 2001; Leigh et al., 2010; Linthorne, 2001; Linthorne and Everett, 2006; Linthorne et al., 2005; Linthorne and Patel, 2011; Red and Zogaib, 1977; Wakai and Linthorne, 2005). In almost all the events studied previously the projection velocity that the athlete can produce decreases as the projection angle is increased. Because the range of a sports projectile is strongly dependent on its projection velocity, this negative relationship between projection velocity and projection angle means that the athlete’s optimum projection angle is substantially less than 45°. An exception is the punt kick by a soccer goalkeeper. In a punt kick the projection velocity of the ball is the same at all projection angles and so the optimum projection angle is about 45° (Linthorne and Patel, 2011). Here, we suggest that the low projection angle that is used in a rugby place kick (about 30°) arises because there is a strong negative relationship between projection velocity and projection angle. The aim of the study reported here was to quantify the relationship between projection velocity and projection angle in a rugby place kick and to see whether this relationship could account for the projection angle that is used (about 30°). We used a video camera to obtain the projection velocity and projection angle of maximum-effort kicks by a male rugby player when performing kicks over a wide range of projection angles. The player’s optimum projection angle for attaining the greatest kick distance was calculated by substituting a mathematical expression for the relationship between projection velocity and projection angle into the equations for the aerodynamic flight of a rugby ball. Our hypothesis was that the player’s calculated optimum projection angle would be in close agreement with his preferred projection angle when kicking for maximum distance. The player’s projection velocity was expected to decrease substantially with increasing projection angle and so his optimum projection angle was expected to be considerably less than 45°. Aerodynamic forces and the requirement to clear the crossbar were expected to have only a small influence on the player’s optimum projection angle (Linthorne and Everett, 2006; Linthorne and Patel, 2011). In a common place kick technique the ball is placed on the ground (supported by a kicking tee, earth, or sand) with its long axis pointing upwards. The kicker uses an approach of about three steps and strikes the ball with the instep of the foot. Many coaches recommend that the goal kicker use the same kicking technique, with near-maximum effort, regardless of the player’s kicking position on the field. For a penalty kick or conversion kick to be successful the ball must pass between the goal posts and over the crossbar. The maximum achievable kick distance is the horizontal distance the centre of mass of the ball travels from the instant of leaving the foot to the instant of reaching the height of the crossbar (Figure 1). The projection variables that determine the kick distance are the projection velocity, v, the projection angle, θ¸, and the height of the crossbar, h (3.0 m; IRB, 2013). ParticipantOne male semi-professional rugby union player (age 21 years, height 1.76 m, body mass 82 kg) volunteered to participate in the study. The study was approved by the Human Ethics Committee of Brunel University, the participant was informed of the protocol and procedures prior to his involvement, and written consent to participate was obtained. The participant wore his own athletic training clothes and football boots.
ProceduresThe kicks were conducted in still-air conditions in an outdoor football facility using an IRB-approved match ball (Synergie; Gilbert Rugby, Robertsbridge, East Sussex, UK). All kicks were performed from a flat artificial grass surface using a standard kicking tee. The participant used three walking steps into the kicking action and performed the kick using the ‘round-the-corner’ style, with the ball making contact with his foot between the toe and the ankle (similar to an instep kick in soccer). A wide range of projection angles was deliberately induced so as to minimize the uncertainty in the mathematical expression that was obtained to describe the relationship between projection velocity and projection angle. The participant performed 18 maximum-effort kicks at his preferred projection angle for attaining maximum distance, and 31 maximum-effort kicks at other projection angles that were ‘higher’ and ‘lower’ than his preferred projection angle. The order of the projection angles was altered to preclude any effect resulting from the order, and an unlimited rest interval was given between kicks to minimize the effects of fatigue on kicking performance. For each kick the horizontal flight distance was measured to the nearest 0.1 m using a fiberglass tape measure. A JVC GR-DVL 9600 video camera (Victor Company of Japan, Yokahama, Japan) operating at 50 Hz was used to record the movement of the ball during the kicks. The video camera was placed at right angles to the kick direction and about 22 m away from the plane of the kick. The field of view was zoomed to allow the participant and ball to be visible throughout the kicking action and for about 10 frames after impact. The movement space of the video camera was calibrated with three vertical poles that were placed along the flight plane of the ball. An Ariel Performance Analysis System (Arial Dynamics, Trabuco Canyon, CA, USA) was used to manually digitize the motion of the center of the ball in the video images. All digitizing was performed by the same operator so as to maximize the consistency of the measured values. The coordinates of the ball were calculated from the digitized data using the two-dimensional direct linear transform (2D-DLT) algorithm.
AnalysisThe projection velocity and projection angle of the ball were calculated using unfiltered ball displacement data from the first six images immediately after impact (Knudson and Bahamonde, 2001). The horizontal component of the projection velocity was calculated as the first derivative of a linear regression line fitted to the ball displacement data, and the vertical component of the projection velocity was calculated as the first derivative of a quadratic regression line (with the second derivative set equal to -9.81 m·s-2) fitted to the ball displacement data (Linthorne and Patel, 2011; Nunome et al., 2006). The projection velocity and projection angle of the ball were calculated using the Pythagorean equation and the trigonometric tangent function. The projection velocity of the ball was plotted against projection angle and a selection of polynomial curves, power curves, and exponential curves were fitted to the data. The most appropriate curve was decided by examining the distribution of the residuals and with calculations of the corrected Akaike’s Information Criterion (Cleveland, 1994; Motulsky and Christopoulos, 2004). An aerodynamic model of the trajectory of a rugby ball was used to calculate the horizontal flight distance in a place kick. We used a rectangular coordinate system where the positive x-axis is in the forward horizontal direction, the positive y-axis is vertically upwards, and the origin is the initial location of the ball. The aerodynamic flight trajectory equations of the ball are then (Linthorne and Patel, 2011)
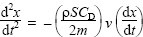 |
(1) |
and
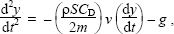 |
(2) |
The flight trajectory of the ball was computed from the initial conditions (i.e., projection velocity and projection angle) using a technical computing software package (Mathematica; Wolfram Research, Champaign, IL, USA). The flight trajectory calculations also required an estimate of the drag area of the ball, SCD. Because of the complex nature of the flight of the ball (the ball tumbles end over end), we calculated the effective drag area of the ball by comparing the measured kick distances with the calculated kick distances (Linthorne and Everett, 2006; Linthorne and Patel, 2011). The drag area in the flight trajectory model was adjusted from 0.020 to 0.030 m2 in increments of 0.001 m2 and the calculated kick distance for each of the kicks was recorded. The drag area that produced best agreement between the calculated and measured kick distances was taken as the effective drag area of the ball. The optimum projection angle for the participant was calculated and compared with his preferred projection angle. To calculate the optimum projection angle the values of the fitted variables were obtained for the curve of best fit for v(θ¸). The resulting equation for v(θ¸) was then used to generate the initial conditions for the flight trajectory equations (equation 1 and equation 2) for a series of projection angles between 0° and 90°. For each projection angle the flight trajectory was calculated and the horizontal flight distance was recorded. The calculated kick distance was plotted against projection angle and the optimum projection angle was the point on the curve at which the kick distance was greatest. We performed kick distance calculations for when the ball reached the height of the crossbar and for when the ball landed on the ground (Figure 1). In this study the uncertainties in the measured values of projection velocity and projection angle arose mainly from the uncertainties in the fit to the coordinate data for the flight of the ball. The uncertainties (95% confidence limits) in the horizontal and vertical components of projection velocity were about ± 0.39 m·s-1 and ± 0.30 m·s-1 respectively, and so the uncertainties were about ± 0.35 m·s-1 for projection velocity and ± 0.7° for projection angle (Kirkup and Frenkel, 2006). The uncertainty in the participant’s optimum projection angle was calculated using the bootstrap method (Efron and Tibshirani, 1993; Linthorne and Patel, 2011).
The values of the kick variables for the 18 kicks at the participant’s preferred projection angle for achieving maximum distance were: distance, 46.8 ± 3.7 m; projection velocity, 26.2 ± 1.7 m·s-1; and projection angle, 30.8 ± 4.6° (mean ± s). For the aerodynamic model of the flight of the ball, best agreement between the measured and calculated kick distances was achieved with a drag area of SCD = 0.028 m2. As expected, the participant’s projection velocity decreased with increasing projection angle (Figure 2). The most appropriate curve for this data was an inverted cubic u-shape centered on θ¸ =00;
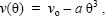 |
(3) |
The calculated values and 95% confidence limits of the fitted variables for equation 3 were vo = 27.9 (±0.8) m·s-1 and a = 8 (±2) x 10-5 m·s-1 per deg3, and the fitted curve is shown in Figure 2a. For a kick in which the ball lands on the ground the participant’s calculated optimum projection angle was 30.6 (±1.9)°, with a kick distance of 45.2 m (Figure 2b). This calculated optimum projection angle value was in close agreement with the participant’s preferred projection angle, 30.8 (±2.1)°. For a kick in which the ball just clears the crossbar the calculated optimum projection angle was 32.3 (±1.9)°, with a kick distance 40.8 m. The optimum projection angle for the player in the present study was similar to projection angles reported for other skilled rugby players. In a study of place kicks by 14 English professional rugby union players, Holmes and colleagues (2006) reported a kick distance (with the ball landing on the ground) of 53.7 ± 5.7 m, a projection velocity of 26.4 ± 3.0 m·s-1, and a projection angle of 30.2 ± 4.4° (mean ± s). The present study confirmed that the optimum projection angle in a rugby place kick is strongly affected by the player’s relationship between projection velocity and projection angle, v(θ¸). For a kick in which the ball lands on the ground the participant’s calculated optimum projection angle (30.6°, ±1.9°) was in close agreement with his preferred projection angle (30.8°, ±2.1°). Therefore, the method used here (finding a mathematical expression for the relationship between the player’s projection velocity and projection angle, then inserting this expression into the aerodynamic model of the flight of the ball) successfully explains the optimum projection angle that is used in a rugby place kick (at least for the player in this study). Figure 3 shows the relative influences of i) the relationship between projection velocity and projection angle, ii) aerodynamic forces, and iii) the height of the crossbar on the optimum projection angle in a rugby place kick. For a non-aerodynamic projectile that is projected at constant velocity (and landing on the ground), the projection angle that produces the greatest horizontal distance is 45°. However, the projection velocity that the player in this study could generate decreased substantially with increasing projection angle, and this relationship reduced his optimum projection angle by 14.0° (to 31.0°). In addition, a tumbling rugby ball experiences substantial aerodynamic drag during its flight through the air. For the player in this study, aerodynamic forces reduced his maximum kick distance by 13.2 m (compared to a kick in a vacuum) but had little influence on his optimum projection angle. (His optimum angle was reduced by only 0.5°.) In a shot at goal the ball must pass over the crossbar. However, this requirement had only a relatively small effect as it reduced the player’s kick distance by 4.4 m and increased his calculated optimum projection angle by 1.7°. Figure 3 shows that the kick distance curve has a relatively broad maximum. This suggests that it is not necessary for the player to kick at close to his optimum projection angle. The curve indicates that when kicking at goal the player in this study could produce a kick distance that is within 5% of his maximum kick distance if he used a projection angle that was within ±6° of his optimum projection angle (32°). The value for the effective drag area of the ball obtained in the present study (SCD = 0.028 m2) was close to that obtained from wind tunnel measurements of a rugby ball when the long axis of the ball is perpendicular to the air flow (SCD = 0.026 m2) (Djamovski et al., 2012). In the present study, the participant’s calculated optimum projection angle was insensitive to the choice of drag area that was used in the aerodynamic flight equations. Drag area values of 0.010 m2 and 0.020 m2 gave a calculated optimum projection angle of 30.9° and 30.7° respectively (with kick distances of 52.7 m and 48.2 m) for a ball that lands on the ground. In this study we did not measure the backspin rate of the ball because the effects of backspin on the kick distance and optimum projection angle were expected to be small. Wind-tunnel data from Seo and colleagues (2007) indicate that as the rate of backspin of a rugby ball is increased from 0 to 10 rev/s, there is almost no change in the drag coefficient of the ball and the lift coefficient increases slightly. Holmes and colleagues (2006) reported a backspin rate of 4.0 ± 0.7 rev/s for place kicks by 14 English professional players. Using a model of a spinning rugby ball (Linthorne and Everett, 2006) and the data from Seo and colleagues (2007), we calculated that for the participant in the present study a backspin of 4 rev/s increases the maximum kick distance by 0.9 m and decreases the optimum projection angle by 0.2° (compared to a kick with almost no backspin). The projection angle used in a place kick (about 30°) is considerably lower than that used in a punt kick (about 45°). This difference is due to differences in the relationship between projection velocity and projection angle, v(θ¸). In a punt kick the player releases the ball from about chest or waist height and the player’s foot strikes the ball when the ball is still well above ground level. The player maintains almost the same kicking mechanics at all projection angles and so the player’s foot velocity at impact is almost the same at all projection angles (Linthorne and Patel, 2011). The projection velocity of a kicked ball is determined mainly by the velocity of the player’s foot at impact (Daish, 1972), and so in a punt kick the projection velocity of the ball is almost the same at all projection angles. This lack of dependence of projection velocity on projection angle means that the optimum projection angle in a punt kick is about 45°. In contrast, the projection velocity of the ball in a place kick decreases substantially with increasing projection angle (Figure 2a) and so the optimum projection angle is well below 45°. The decrease in ball projection velocity observed in the present study when kicking at high projection angles was probably due to changes in the player’s kicking mechanics that resulted in a lower foot velocity. However, we did not investigate the player’s kicking mechanics in this study because a 2-D video analysis was not expected to produce reliable kinematic data for limb movements that are not in the plane of the flight of the ball (Bezodis et al., 2007). Generalization from a single participantInitially, the most substantial limitation of the present study appears to be that only one participant was analyzed. However, the results from this study can still be generalized and we argue that most skilled male rugby players can be expected to have optimum projection angle of about 30°. The argument for generalization is based on three key findings from previous studies of the optimum projection angle in other sports (most of which analyzed several participants): 1) The change in projection velocity with increasing projection angle was a continuous function and had no ‘jumps’ or discontinuities. This indicates that the participants made only minor systematic changes to their technique in order to change the projection angle. 2) The mathematical form of the relationship between projection velocity and projection angle v(θ¸) was the same for all the participants in the study. This indicates that the techniques used by the participants were basically the same and shared the most important features. 3) Within a study there were inter-subject differences in the rate of change in projection velocity with increasing projection angle. These differences were reflected as differences in the fit parameters for v(θ¸), and resulted in slight differences in optimum projection angle among the participants. In the present study on the rugby place kick, the relationship between projection velocity and projection angle was clearly a continuous function (Figure 2a). Note also that the participant had a preferred projection angle (30. 8°) that was similar to the mean value (30.2°) in the study of English professional rugby union players by Holmes and colleagues (2006). This suggests that the kicking technique used by the participant in the present study was essentially the same as that used by the English professional players. In the present study the standard deviation in projection angle for the kicks at the participant’s preferred projection angle (4.6°) was similar to the standard deviation in projection angle for the 14 English professional players (4.4°). This indicates that the observed inter-subject differences in projection angle for the English professional players were mostly due to intra-subject variations in projection angle, rather than due to real differences in optimum projection angle among the players. Therefore, we conclude that most skilled male rugby players can be expected to have a v(θ¸) relationship that is similar to that for the participant in the present study, and hence can be expected to have an optimum projection angle of about 30°.
Simulations for players of varied physical characteristicsWe used mathematical modeling to further investigate the effect of inter-subject differences in the v(θ¸) relationship on the optimum projection angle. When comparing players using equation 3, we expect that the projection velocity for a horizontal projection angle (vo) would differ substantially among players because of differences in muscular strength, but the measure of the curvature (a) would be roughly the same for most players if they have similar kicking mechanics. Figure 4 shows the calculated effects of changes in vo and a on the player’s optimum projection angle (for a ball that just clears the crossbar). A greater maximum projection velocity (vo) produces a greater maximum kick distance, but has little effect on the player’s optimum projection angle; whereas a greater curvature (a) reduces the player’s optimum projection angle, but has little effect on the maximum kick distance. However, note that substantial changes in curvature produce only modest changes in optimum projection angle. These calculations indicate that the optimum projection angle for most skilled male rugby players should be similar to that for the participant in the present study (i.e., around 30°).
This study showed that a player’s optimum projection angle in a rugby place kick can be calculated by substituting the mathematical expression for the player’s relationship between projection velocity and projection angle into the equations for the aerodynamic flight of a rugby ball. The projection velocity that a player can produce decreases substantially as projection angle is increased, and this relationship reduces the player’s optimum projection angle to well below 45°. Aerodynamic forces and the requirement to clear the crossbar have little effect on the optimum projection angle. For the player in this study the optimum projection angle (for a ball that clears the crossbar) was 32°. |
| AUTHOR BIOGRAPHY |
|
 |
Nicholas P. Linthorne |
| Employment: Centre for Sports Medicine and Human Performance, School of Sport and Education, Brunel University, UK. |
| Degree: |
| Research interests: Physics and mathematics in track and field athletics and football. |
| E-mail: nick.linthorne@brunel.ac.uk |
| |
 |
Thomas G. Stokes |
| Employment: Undergraduate student at Brunel University. Now at Christ’s Hospital School, West Sussex, UK. |
| Degree: BSc (Hons) |
| Research interests: Biomechanics of rugby. |
| E-mail: tgs@christs-hospital.org.uk |
| |
|
| |
| REFERENCES |
 Bezodis N., Trewartha G., Wilson C., Irwin G. (2007) Contributions of the non-kicking-side arm to rugby place-kicking technique. Sports Biomechanics 6, 27-31. |
 Cabri J., De Proft E., Dufour W., Clarys J.P., Reilly T., Lees A., Davids K., Murphy W.J. (1988) Science and football. The relation between muscular strength and kicking performance. London:. E & FN Spon. |
 Cleveland W.S. (1994) The elements of graphing data. Summit. Hobart Press. |
 Daish C.B. (1972) The physics of ball games. London. English Universities Press. |
 Djamovski V., Rosette P., Chowdhury H., Alam F., Steiner T. (2012) A comparative study of rugby ball aerodynamics. Procedia Engineering 34, 74-79. |
 Efron B., Tibshirani R.J. (1993) An introduction to the bootstrap. Boca Raton, FL. CRC Press. |
 Holmes C., Jones R., Harland A., Petzing J., Moritz E.F., Haake S. (2006) The engineering of sport 6 (Vol. 1). Ball launch characteristics for elite rugby union players. New York. Springer. |
 Hubbard M., de Mestre N.J., Scott J. (2001) Dependence of release variables in the shot put. Journal of Biomechanics 34, 449-456. |
 IRB. (2013) Rugby union: Laws of the game. Dublin. International Rugby Board. |
 Kirkup L., Frenkel R.B. (2006) An introduction to uncertainty in measurement. Cambridge. Cambridge University Press. |
 Knudson D., Bahamonde R. (2001) Effect of endpoint conditions on position and velocity near impact in tennis. Journal of Sports Sciences 19, 839-844. |
 Leigh S., Liu H., Hubbard M., Yu B. (2010) Individualized optimal release angles in discus throwing. Journal of Biomechanics 43, 540-545. |
 Linthorne N.P. (2001) Optimum projection angle in the shot put. Journal of Sports Sciences 19, 359-372. |
 Linthorne N.P., Everett D.J. (2006) Release angle for achieving maximum distance in the soccer throw-in. Sports Biomechanics 5, 243-260. |
 Linthorne N.P., Guzman M.S., Bridgett L.A. (2005) Optimum projection angle in the long jump. Journal of Sports Sciences 23, 703-712. |
 Linthorne N.P., Patel D.S. (2011) Optimum projection angle for attaining maximum distance in a soccer punt kick. Journal of Sports Science and Medicine 10, 203-214. |
 Motulsky H., Christopoulos A. (2004) Fitting models to biological data using linear and nonlinear regression. Oxford. Oxford University Press. |
 Nunome H., Ikegami Y., Kozakai R., Apriantono T., Sano S. (2006) Segmental dynamics of soccer instep kicking with the preferred and non-preferred leg. Journal of Sports Sciences 24, 529-541. |
 Red W.E., Zogaib A.J. (1977) Javelin dynamics including body interaction. Journal of Applied Mechanics 44, 496-498. |
 Seo K., Kobayashi O., Murakami M. (2007) Aerodynamic characteristics of a rugby ball spinning on its transverse axis. Transactions of the Japan Society of Mechanical Engineers Series B 73, 1999-2003. |
 Wakai M., Linthorne N.P. (2005) Optimum takeoff angle in the standing long jump. Human Movement Science 24, 81-96. |
|
| |
|
|
|
|

