|
|
|
| |
| ABSTRACT |
|
Despite the importance of maintaining good alignment to minimize resistive drag in swimming there is a paucity of literature relating to the effect of technique asymmetries on rotations of the body about a vertical axis (yaw). The purpose of this paper was to present an approach to analyzing the effect of technique asymmetries on rotations in swimming, exemplifying the process with a case study of a breaststroke swimmer. The kinematics and angular kinetics of an elite female international breaststroke swimmer performing a ‘fatigue set’ of four 100m swims were derived from digitized three-dimensional video data using a 13 segment body model. Personalised anthropometric data required to quantify accurately segment and whole body centres of mass and segmental angular momentum were obtained by the elliptical zone method. Five episodes of torques producing yaw occurred in the stroke cycle sampled for each 100m swim of this swimmer. These torques were linked to bilateral differences in upper limb kinematics during 1) out-sweep; 2) in-sweep; 3) upper limb recovery; and lower limb kinematics during 4) Lower limb recovery and 5) the kick. It has been shown that by quantifying whole body torques, in conjunction with the kinematic movement patterns, the effect of technique asymmetries on body alignment can be assessed. Assessment of individual swimmers in this manner provides a solid foundation for planning interventions in strength, flexibility, and technique to improve alignment and performance. |
| Key words:
Asymmetry, human swimming, hydrodynamic drag, yaw
|
Key
Points
- A unique (not been attempted previously) study of yaw in breaststroke swimming that yields new knowledge of how technique and strength asymmetries affects body alignment.
- Establishes an approach to investigation of yaw in swimming using 3D videography and inverse dynamics.
- Exemplifies the approach with a case study. The case study illustrated the potential of the approach to enable detailed assessment of yaw and to explain how the yaw is produced in terms of the asymmetries in speed and magnitude of the swimming actions.
- This procedure should be used to identify and quantify asymmetries that might impair performance.
|
One of the fundamental principles of swimming is to minimise resistance by maintaining good alignment between the longitudinal axis of the body and the intended line of progression (Counsilman, 1973; Maglischo, 2003). Thus, the prone swimmer seeks to progress in the swimming direction and avoid rotations of the body about a vertical axis of the external reference frame (yaw) so that the body remains aligned with the swimming direction. While many studies have looked at the effect of body roll on performance in front crawl, for example, Lui et al. (1993), Payton et al. (1997), Cappaert et al. (1998), Castro et al. (2003), Yanai (2004), Seifert et al. (2005), Castro et al. (2006), Psycharakis and Sanders (2008), Sanders and Psycharakis (2009), Psycharakis and Sanders (2010), Psycharakis and McCabe (2011), Payton and Sanders (2011) little research has been conducted to investigate yaw in human swimming. Yaw occurs when torques about the vertical axis produced by the limbs on one side of the body are not balanced by those on the other side of the body. In the ‘symmetrical strokes’ that is, breaststroke and butterfly, the torques produced by right and left hands and those produced by right and left feet can balance so that there is zero net torque about the vertical axis throughout the stroke. However, if asymmetries in the magnitude of force and its moment arm exist due to bilateral differences misalignment will occur. An early study of breaststroke swimmers (Czabanski and Koszcyc, 1979) revealed that technique asymmetry is very common. Carson (1999) reported a case study of an 11 year old competitive swimmer whose breaststroke technique was so asymmetrical in its movement pattern that he was being repeatedly disqualified. Physical examination revealed strength asymmetries in the shoulders and hips which reflected postural asymmetries and asymmetrical muscle tightness. Carson (1999) reported that therapeutic interventions resulted in improved muscle balance, posture, movement patterns, and race performance. In our recent analyses of five elite breaststroke swimmers some asymmetries were evident in the techniques of all five swimmers. However, the severity of the asymmetries and likely impact on performance varied greatly among the swimmers. Further, the nature of the technique asymmetries differed among the swimmers. Work needs to be done to understand the effects of asymmetries on performance to inform decisions on whether interventions to correct asymmetries are warranted. Some asymmetries may not affect performance and so interventions to remove them might be counter-productive and interfere with the swimmer’s training program. On the other hand, if asymmetries in strength, flexibility, or technique produce torques that cause poor alignment and increase resistance it may be worthwhile to introduce programs such a strength training, physiotherapy, and technique training to correct the asymmetries. Bilateral strength differences have been recognised as contributing to asymmetries in swimming actions (Sanders, 2013; Sanders, Thow, and Fairweather, 2011; Sanders et al., 2012). For example, Tourney-Chollet, Seifert, and Chollet (2009) have observed that bilateral differences in isokinetic strength of medial rotator shoulder muscles force symmetry of right and left sides are related to bilateral differences in phase durations in front crawl swimming. Further, it is well known that changes in the three-dimensional kinematics of swimming occur as the swimmer’s capacity to produce force declines with fatigue (Figueiredo et al. 2012; 2013). However, there is an extreme paucity of data in the extant literature identifying technique asymmetries and their effect on alignment of the body through the production of torques. This is partly due to the difficulty of calculating torques acting on a swimmer interacting with a fluid environment. In one of the very few quantitative studies of torques acting on a swimmer Yanai (2004) applied the model of Dapena (1978) to determine the role of the buoyancy force in generating body roll in front crawl swimming, concluding that buoyancy is the primary source of generating body roll in front crawl swimming. However, there is a dearth of data relating to the possible effect of technique asymmetries in producing unbalanced torques that cause yawing motion. In studying contributions to performance, the usual practice is to identify commonalities in kinematics and kinetics associated with performance. Naturally, the ideal approach for this is to obtain data from a sample of swimmers who perform at an elite level or to compare elite and sub elite either by comparing groups or using regression analysis to identify what changes with increasing levels of performance. However, when diagnosis of the limitations and constraints that prevent an individual swimmer from adopting an optimal kinematic and kinetic pattern is required, a case study approach is appropriate. In particular if a swimmer’s alignment is disrupted there are myriad possible causes. Thus, the goal of the analysis is to identify the cause of the misalignment for that particular swimmer. Aetiologies include asymmetries in body shape, bilateral strength differences, and bilateral differences in flexibility (Sanders, Thow, and Fairweather, 2011). Further, a swimmer who may have had good swimming technique, may develop faults due to the effect of imbalances arising from training practices or injuries. In this paper we illustrate by way of an in-depth case study how asymmetrical segmental motions are linked to the production of torques that contribute to yawing motions of a breaststroke swimmer. The paper exemplifies a process of analysis that can be applied in future studies to increase understanding of how technique asymmetries can influence body alignment in swimming. ParticipantsOne elite female breaststroke swimmer (height: 1.78 m; weight: 69.8kg) who competes internationally in 50 m and 100m events was selected for in-depth analysis due to the presence of a consistent pattern of yawing motions. Her personal best time for 100m long course is 1.10.85. She is right side dominant (both arm and leg) and when training front crawl she breathes predominantly to the right. At the time of testing she was free of injuries but had, in the past, injuries to ankles, knees, and left intercostal muscle.
Collection of strength dataDynamic strength data for shoulder flexion/extension, shoulder internal/external rotation, and knee flexion/extension were collected on a Biodex Dynamometer (Biodex®, Biodex Corporation, Shirley NY.). These actions are known to be prominent in swimming (Miyashita and Kanehisa, 1979; Payton et al., 1997; Payton et al., 2002). The Biodex was set to ‘isokinetic mode’ with constant speeds of 60°/s and 180°/s. A rotational speed of 60°/s is one of the most accepted to measure the peak torque of participants (Campenella et al., 2000; Girold et al., 2006; 2007; Lephart et al., 2002; Lund et al., 2005; McCleary and Andersen, 1992; Stickley et al., 2008). A rotational speed of 180°/s enables assessment of torques that can be applied at rotation speeds similar to those used in actual swimming where, for example, based on our data, the shoulder joints typically flex through approximately 90 degrees in approximately 0.5s in the trials of this breaststroke swimmer. While the knee joint angular velocities commonly exceeded 180°/s accuracy of the measures obtained on the Biodex dynamometer diminishes at speeds higher than 180°/s (Mayer et al., 2001) meaning that 180°/s is the upper limit of the speed range for obtaining accurate and reliable results. Following familiarisation and warm-up, twelve repetitions of each exercise were performed at maximum effort, first at 60°/s followed by 180°/s conducted in accordance with the standard operating guidelines issued by Biodex Inc. The order with respect to right and left was randomised. Asymmetry in dynamic strength across right and left sides was indicated by a difference in average peak torque at each rotation rate and expressed as a percentage of the higher of the two values. Given that the swimmer’s results were to guide strength and conditioning and physiotherapy programs the swimmer was highly motivated to comply with the instructions ‘push as hard and as fast as you can for every repeat’. The Biodex is known to be reliable among motivated subjects with ICCs of 0.95 at 60°/s and 0.96 at 180°/s reported for peak torque during knee flexion and extension (Feiring et al., 1990).
Collection of anthropometric dataThe participant, wearing a one piece legless racing competition swimsuit complying with the new rules (i.e. not a body suit) was photographed simultaneously by two digital cameras at a distance of 10m capturing orthogonal front and side views of the subject in accordance with the ‘e-Zone’ method described by Deffeyes and Sanders (2005). A bespoke MATLAB program, based on Jensen’s (1978) ‘elliptical zone’ method, was used to determine the segment masses, segment centre of mass positions relative to the segment endpoints, and moments of inertia about transverse, antero-posterior, and longitudinal axes of each segment from the digitised landmarks. Briefly, masses segment masses and moments of inertia are based on the volume of the segment modelled as a series of ellipses with depth of 2cm. Using the diameters of the each ellipse obtained from the digitised front and side photographs in conjunction with estimates of density, the mass of each ellipse can be found. The position of the centre of mass of the segment relative to a meaningful landmark or segment endpoint can then be determined by summing moments and the moments of inertia about the three anatomical axes of the segment determined by summing the local and remote terms of the contributions of each ellipse by applying the parallel axis theorem (Hay, 1993). These methods have been applied in several three-dimensional studies of swimming (Psycharakis and Sanders, 2008; Psycharakis and McCabe, 2011; Sanders and Psycharakis, 2009). The e-zone method enables the characteristics of the segments of the individual swimmer to be taken into account when calculating segmental contributions to torques about the three body axes. Reliability of repeated digitisations of the photographs has been assessed (paper under review). Coefficients of variation are less than 1% for segment centre of mass locations and masses of the trunk and thorax, less than 2% for the moments of inertia about the transverse and anteroposterior axes, and less than 3% for the moment of inertia about the longitudinal axis. CVs for the smaller body segments are larger, for example, the forearms have CVs of approximately 2% in segment centre of mass location, 5% in mass, and 8% in moments of inertia. However, due to their much smaller mass and moments of inertia, these have only small effects on the whole body net torques. These e-zone data were then input to the MATLAB analysis program enabling calculation of whole body centre of mass, whole body velocity and acceleration, angular momentum and torque. To enable identification of the endpoints of body segments when digitising the video recordings, black skin markers 1.5cm in diameter were applied to 19 anatomical landmarks. Marker locations were: the vertex of the head (using a swim cap), the right and left of the following: tip of the 3rd distal phalanx of the finger, wrist axis, elbow axis, shoulder axis, hip axis, knee axis, ankle axis, 5th metatarsophalangeal joint, and the tip of 1st phalanx (big toe). These markers defined a 13 segment body model for whole body CM calculation comprising the combined head and neck, thorax and trunk as a combined segment, right and left arms, forearms, hands, thighs, shanks, and feet. The head and neck was combined as a single segment for calculation of linear and angular kinematics and kinetics. Similarly the thorax and abdomen were combined as a single segment (referred to as the ‘trunk’) for calculation of linear and angular kinematics and kinetics. However, because the hips and shoulders rotate somewhat independently about the long axes of the thorax and abdomen respectively angular kinematics and kinetics of the thorax and abdomen about their longitudinal axes were calculated separately.
Testing procedureThe swimmer performed her usual warm-up prior to the testing session for a period of five minutes. The testing required the swimmer to perform a ‘fatigue set’ comprising 4*100m maximum effort breaststroke swims from a push start with no pacing strategy. Successive 100m swims commenced 90 seconds apart ensuring short and diminishing rest time between 100m swims. This was designed to enable assessment of whether technique changed as a consequence of increasing fatigue. The testing session was conducted in a 25m x 13.25m x 2m indoor level deck swimming pool (average pool temp 29.5° ± 0.2). The volume within which the data were sampled was calibrated using a rectangular prism frame 4.5m in length (X direction), 1.5m height (Y direction), and 1.0m width (Z direction) (Psycharakis, Sanders, and Mill, 2005). The frame was suspended so that half was below and half above the water surface with the X axis aligned with the swimming direction. The calibration frame was recorded by six gen-locked Elmo PTC-400C PTZ cameras (four cameras below and two above the water surface) and digitised to yield separate calibration files for the above and below water views using the Ariel Performance Analysis System (APAS) which incorporates the direct linear transformation (DLT) algorithms of Abdel-Aziz and Karara (1971). The heights of all cameras were adjusted so that the control points on the calibration frame were clearly distinguishable. All six cameras recorded the motion of the swimmer at a sampling frequency of 25 frames per second and an electronic shutter speed of 1/120s enabling sharp images of the moving limbs for digitising.
Data processingOne breaststroke stroke cycle (SC), defined as the period between the instant of commencement of lateral movement of the hands (Z direction) for the out-sweep to the corresponding instant in the next stroke, was selected from the third lap of each 100m swim. The third lap was chosen as the calibrated space was further from the turning wall for the odd numbered laps than the even laps, thereby ensuring that the swimmer was well into their mid-pool phase and unaffected by the turn. Using the third lap rather than the first ensured that the sample was taken at a time when they were in the phase of the swim in which the pace is almost constant and intracyclic variability is small. APAS was used to manually digitise the nineteen body landmarks separately for above and below water views for every video field from all six camera views. The digitised data set comprised 10 frames prior to, and beyond, the defined SC to avoid subsequent endpoint errors when processing the data. Following DLT transformation of the data into 3D coordinates the above and below water coordinate data were then combined into one single file representing continuous coordinates throughout the SC. This file was input to a customised MATLAB analysis program to calculate all variables. During this process a 4th order Butterworth filter with a frequency cut off of 4 Hz was applied after extrapolating the data by reflection to an additional 20 points beyond the start and finish of the SC (30 fields of additional data at each end) as added insurance against distortion of the endpoints of the data set. The rationale for choosing 4 Hz as the cut-off was based on the Fourier spectral analysis indicating that little power (<1%) was contained in frequencies greater than 4Hz. Also, the frequency cut-off complies with the ‘rule of thumb’ to sample at least five times the highest frequency of interest to avoid aliasing. A Fourier transform and inverse transform was then used to interpolate the data to the equivalent of 200 samples per second to increase the precision of identifying the start and finish of the SC. After trimming the data to the period of the SC the data were then converted to 101 points, again by Fourier transform and inverse transform, representing percentiles of the SC. The use of the Fourier series transform is regarded as highly appropriate when analysing periodic data, such as in swimming (Bartlett, 1997).
Data analysisThe whole body centre of mass (CM) was determined by taking moments about the X, Y, Z reference axes of the segment centres of mass obtained using the digitised endpoint coordinates in conjunction with the segment masses and proportional segment centre of mass locations obtained from the e-Zone program. Paths of the hands, represented by the wrists, and paths of the feet, represented by the ankles, were expressed relative to the CM. Linear and angular segmental kinematics were determined from the digitised segment endpoint coordinates using standard inverse dynamics approaches. The angle of yaw of the trunk was determined as the angle between the projection onto the XZ plane of the position vector (v) of the midpoint of the shoulders with respect to the midpoint of the hips and the X axis. Computationally this was:
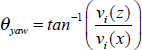 |
Eq 1 |
Where v i(z) and v i(x) are the Z and X components of v respectively at the ith time percentile.
The angular momentum vector (H) of each segment (s) was calculated as the sum of local (HL) and transfer (HT) terms calculated using the methods of Dapena (1978). The components of the angular momentum vector represent rotations about the external horizontal X axis (roll), the vertical Y axis (Yaw) and the horizontal Z axis (pitch). To calculate the local angular momentum contribution (HL) the angular momentum of the segment about an instantaneous axis of rotation perpendicular to the long axis of the segment was determined as:
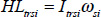 |
Eq 2 |
Where HL trsi is the local angular momentum of segment s about its own transverse axis at the ith time percentile expressed in the external reference system; I trs is the moment of inertia of segment s about its transverse axis obtained from the e-Zone program (Deffeyes and Sanders, 2005) and y si is the angular velocity vector of segment s at the ith time percentile.
To obtain the angular velocity vector an orientation vector was defined as the unit vector (R) in the direction of the long axis of the segment. The magnitude of the angular velocity of the segment was:
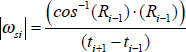 |
Eq 3 |
Where t i is the time at the ith percentile. The angular velocity vector was then
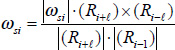 |
Eq 4 |
This yields an angular velocity vector perpendicular to the plane determined by Ri+1 and Ri-1. Angular momentum of the limb segments about their longitudinal axes was regarded as negligible relative to the magnitude of the angular momentum about their transverse axis and therefore ignored in accordance with Dapena (1978). Given that the upper and lower torso are large segments that rotate about their longitudinal axis in swimming (albeit not deliberately in breaststroke swimming) angular momenta of those segments about their long axes were calculated. The same process described above was applied except that the orientation vectors were the line between the shoulders for the upper torso and between the hips for the lower torso. It was deemed necessary to treat the trunk as two segments comprising upper torso (including the head and neck) and lower torso when assessing angular momentum about the long axis due to the relative independence of hip and shoulder rotation in swimming (Cappaert, 1998; Payton et. al., 1999; Psycharakis and Sanders, 2008). The anatomical division of the upper and lower torso was the plane perpendicular to the long axis of the body passing through the xiphoid process. Moments of inertia of these segments about their long axes were obtained from the output of the e-Zone program. The angular momentum of the whole trunk (including the head and neck) was then the vector sum of local and transfer terms of the combined trunk segment about its instantaneous transverse axis, and the local and transfer terms of the upper and lower torso about their long axes. The contributions of the transfer components to angular momentum about each of the orthogonal axes of the external reference frame were computed using:
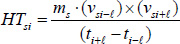 |
Eq 5 |
Where HT si is the transfer term of the angular momentum of segment s at the ith time percentile and v si is the vector obtained by subtracting the location of the segment centre of mass from the CM.
Torque at the ith time percentile acting on each segment s was determined as:
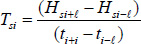 |
Eq 6 |
Consistency of the time seriesTo provide an indication of how consistent the normalised time series were across the fatigue set a repeatabililty coefficient (r) was calculated (Kadaba et al., 1989).
StrengthThe average peak torque obtained from the Biodex Dynamometer for each exercise and speed are shown in Table 1. The right knee was stronger than the left in knee extension at both 60°/s (9%) and 180°/s (15%). The right side was stronger than the left in knee flexion at 60°/s (17%) but not at 180°/s. Differences between right and left sides in shoulder internal and external rotation were small except for internal rotation at 180°/s (8.1%). The right shoulder was stronger than the left in flexion and extension at both speeds by magnitudes between 5% and 10%. These differences need to be considered in the light of what is common in terms of asymmetry.
Asymmetry of Upper and Lower Limb ActionsFigure 1 and Figure 2 show the Z positions with respect to the midline of the body (line from midpoint of the hips to midpoint of the shoulders) of the wrists and ankles respectively plotted against time normalised to percentiles of the SC defined as the period between the first instant of outward movement of the wrist until the same instant in the next SC. These figures are useful in showing the differences in the width of the pull and kick between right and left sides, the timing of the phases of the stroke, and the differences in timing between right and left sides with successive 100m swims. The timing of the transition between the out-sweep and in-sweep of the hands coincides with the instant of attaining the widest points and the commencement of recovery is evident as the time when the wrists stop moving rapidly towards the midline (Figure 1). The swimmer slowed as the set progressed due to the effect of fatigue reflected in the times for each 100m (Ist: 1:16.60; 2nd: 1:19.19; 3rd: 123.22; 4th: 127.65). The actual duration of the SCs were 1.49s, 1.46s, 1.62s, 1.73s, with the differences due primarily to an increase in the time from commencement of the kick to the start of hand separation as the swimmer became fatigued. Thus, when represented as normalised time, the events in the 3rd and 4th 100m swims occur at a smaller percentage of the SC than the events in the 1st and 2nd swims. Despite the changes in duration of the SC the patterns remain very similar within sides of the body (right wrist: r = 0.985; left wrist: r = 0.986; right ankle: r = 0.956; left ankle: r = 0.967)
Trunk YawFigure 3 shows the trunk yaw profiles across normalised time of the sampled SC for each of the 100m swims. Patterns of trunk yaw were similar across the fatigue set (r = 0.900). The pattern comprised a slight yaw to the left (indicated by positive yaw angles corresponding to anti-clockwise rotation) during the out-sweep of the hands, a yaw to the right (indicated by negative yaw angles corresponding to clockwise rotation) during the in-sweep, a rotation to the left during recovery of the upper limbs followed by a rotation to the right to realign the trunk with the line of swimming direction during flexion of the hips and knees in preparation for the kick. Taking into account the change in duration of the SC across the four swims the yaw patterns were very similar except that the yaw to the left in the second half of the stroke cycle was less in the 3rd and 4th swims than in the 1st and 2nd swims.
Whole body angular momentumFigure 4 shows the whole body angular momentum across the sampled SC for each of the 100m swims. Apart from the timeline differences associated with the increased duration of the glide following arm recovery, the patterns were very similar (r = 0.859). However, angular momentum reflecting yawing motion to the left during the arm recovery diminished with fatigue.
Whole body torqueFigure 5 shows the net torque acting on the whole body. The timing of the torques indicates the link between the actions and the changes in angular momentum. Common trends were apparent across the fatigue set (r = 0.786). During the out-sweep of the hands, the torques were generally positive and therefore developed angular momentum to produce some yaw to the left. During the in-sweep the torques became strongly negative, changing the angular momentum to negative and consequent yaw to the right. A large positive torque coincided with the commencement of the recovery of the upper limbs and eventually reversed the direction of rotation. A negative torque acting to bring the body back into alignment occurred during the recovery of the lower limbs in preparation for the kick. The torques became smaller in the 3rd and 4th 100m swim than in the first two 100m swims.
By establishing methods of quantifying trunk yaw, whole body angular momentum about the vertical axis, and the torques that cause the yawing motion, a foundation for understanding how asymmetrical segmental motions are linked to the yawing motions of a breaststroke swimmer has been established. It is anticipated that this will lead to an increased understanding of swimming in a similar manner to the advancement of the understanding of complex athletic events such as high jumping (Dapena, 1980). The method requires that segment and whole body centres of mass, and segment moments of inertia are determined with small error. To achieve that goal, these measures were obtained using the elliptical zone method (Jensen, 1978) with digitising and calculation software developed by Deffeyes and Sanders (2005). This ensured that the data took into account the shape and mass distribution of this particular swimmer. The process of applying the method to diagnose misalignment was illustrated with a case study of a breaststroke swimmer. This process would inform an intervention to correct the problem and improve the swimmer’s technique and performance. The method could be applied in a similar way to diagnose misalignment due to torques about any of the three principal axes of a swimmer. Application to breaststroke swimming, as in the case of this swimmer, was of particular interest because the swimmer had been competing at an elite level in a stroke that is expected to be symmetrical with little or no tendency to rotate about a vertical axis (yaw). Nevertheless, this high level swimmer had approximately 5° of trunk yaw to both right and left sides throughout the various stroke phases that was linked to asymmetrical technique characteristics yielding a repeated pattern across the four 100m swims. This was despite the desirability of maintaining good alignment of the trunk with the direction of intended motion. The fact that the undesirable movement pattern was repeated consistently across four 100m swims indicated that the asymmetries in technique have become automated. The characteristics of that movement pattern and how they are linked to the production of yaw were explored so that an intervention to correct the technique can be planned and implemented so that the swimmer could realise her potential. Five main imbalances in net torque were identified: 1) Positive Torque during the Out-sweep: Figure 1 reveals some asymmetries between right and left wrist motion in the lateral (Z) direction. The right hand started closer to the midline than the left and moved slightly wider than the left. The most lateral position was also attained 2-3% sooner by the right hand than the left. Thus, the right hand was moving faster than the left (Table 2). Consequently, assuming that both hands were oriented to produce maximum force, it is likely that the right hand would be generating larger reaction forces from the water than the left (Sanders, 1999). Given that the moment arms of the forces were large due to the remote locations of the hands with respect to the CM a modest difference in forces generated by right and left hands created a torque to produce some yaw to the left. The larger and faster movement of the right hand may be linked to right side dominance and to greater strength on the right side than the left as evident from the Biodex results (Table 2). Another possibility is that the movement pattern was habituated during the period of left intercostal injury. This possibility of automisation of sub-optimal movement patterns associated with injury and their persistence after full injury recovery has been documented in a case study by Collins, Morriss and Trower (1999) for an elite javelin thrower. 2) Negative Torque during the In-sweep: Figure 1 shows that during the in-sweep the right hand moved through a larger range of motion than the left and finished the in-sweep closer to the midline of the body than the left. Thus, the right hand moved faster (Table 3) and may have generated larger forces than the left yielding large net torques and angular motion to the right. The greater force applied by the right hand is interesting given that shoulder internal rotation is a major part of the in-sweep action and yet the testing on the Biodex (Table 1) did not show differences in strength of the right and left shoulders in internal rotation at the 60°/s speed. However, at 180°/s of internal rotation, a closer match to the rates of angular rotation used during the in-sweep, the right shoulder was 8.1% stronger than the left. It is also interesting that the left hand did not move towards the midline as much as the right. Therefore, in addition to possibility of increased strength of the right shoulder being a contributing factor to the production of yaw during the in-sweep, the observed asymmetry in hand path may be linked to habituation of a restricted in-sweep of the left hand during the period which the swimmer was affected by the intercostal injury. Development of asymmetries in movement patterns through habituation and side dominance are common in swimming. For example, Seifert et al. (2008) have shown that front crawl swimmers who have a definite preferred breathing side are more likely to have spatial and temporal technique asymmetries than swimmers who are habitual bilateral breathers. Further, Psycharakis et al. (2008) have shown that swimmers roll more to their preferred breathing side even when swimming without breathing. Although breathing is not performed to the side in breaststroke, these studies show that habituation of asymmetrical movement patterns transfers to asymmetrical movement even when the stimulus for asymmetrical movement is no longer present. Therefore, it is possible that the pattern of movement of the left upper limbs during the period of left intercostal injury of the breaststroke swimmer in this case study persisted after the injury ceased to exist. 3) Positive Torque during Recovery of the Upper Limbs: Three sources of evidence indicate that the positive torque during the recovery of the upper limbs was due to the orientation and motion of the upper limbs. Figure 6 shows the angular momentum of the trunk, arms, forearms, thighs, shanks, and feet for the sample from the first 100m swim. It is apparent that during the period of positive torque i.e. from between approximately 50 to 80% of the cycle, the timing of angular momentum changes was similar in terms of direction for all body segments except the forearms. That is, the whole body was responding to the external torques and the angular momentum of the body segments was changing with similar timing. Conversely, the angular momentum of the forearms was opposite in phase to that of the other body segments. The forearms had positive angular momentum at the end of the in-sweep and then negative angular momentum as they recovered forward. This implies that the motion of the forearms was causing the torques that rotated the other body segments in the opposite direction. The forearms were swinging to the right, pushing against the water on their right side and thereby generating reaction forces to the left. Consequently, an external torque to the left due to the action of the forearms created anticlockwise angular motion of the other body segments. The second source of evidence is the asymmetrical pattern of lateral motion of the wrists during the recovery phase as evident in Figure 1. The left wrist started its recovery a considerable distance to the left of the midline and gradually moved to the right to finish close to the midline. The right wrist moved to the midline and then slightly to the right. Again, this indicates that the upper limbs were pushing water to the right, creating a force from the water acting to the left and thereby generating positive torques The third source of evidence is linked to the angular orientation of the forearms shown in Figure 7. At the end of the in-sweep and beginning of recovery the angle of the right arm to the X axis reached a maximum of about 45 degrees whereas the angle of the left forearm to the X axis was only about 30 degrees. This means that as the forearms moved forward and rotated towards an aligned and streamlined position, the net resistive force in reaction to that motion acted to the left and, as a consequence, a torque in the positive direction. 4) Negative torque prior to the kick: A torque from about 80% of the SC coincided with hip and knee flexion prior to the kick. During this period of the SC resistive forces would have been large due to the non-streamlined posture. Figure 2 shows that the Z position of the right ankle (0.4m) was wider than the left (0.3m) ankle prior to the kick. Thus, it would be expected that although the resistive forces could be similar on both sides of the midline, the moment arm on the right side was greater. Thus, there was an unbalanced torque causing rotation to theright. This interpretation is supported by Figure 8 showing the projected angles of the thigh. The right thigh had swung outwards from the midline more than the left. Thus, the resistive forces acting against it had a larger moment arm than those acting on the left thigh. 5) Positive torque during the kick: During the kick the right foot had a wider path than the left (Figure 2). Therefore, the propulsive forces produced by the right foot had a greater moment arm than those of the left. Average foot speeds during the kick were between 11 and 23% greater for the right foot than the left. This would have generated larger propulsive forces on the right side than on the left side further increasing the magnitude of net positive torque. The greater speed of right foot motion than the left is in keeping with greater knee extension strength and right side dominance. ImplicationsThrough application of the methods described in this paper, the causes of rotations in aquatic activities of individuals, in this case yaw of an elite breaststroke swimmer, can be traced. Asymmetries in technique were shown to be linked to the torques causing the yaw. Once the technique asymmetries have been identified, programs to ameliorate the asymmetries can be implemented. In this case, habituation of movement patterns, in particular, the left upper limbs being different from the right upper limbs, may be linked to several causes including injury to an intercostal muscle on the left side, right side dominance, and strength differences. It is unclear whether the pattern of lower limb motion emanates from the yawing actions created by the technique asymmetries of the upper limbs. It may be, for example, that the right lower limbs swinging wider than the left in preparation for the kick may be due in part to the yaw to the left that occurs in response to the asymmetrical recovery of the upper limbs. While further dry land training can be done to ensure that strength asymmetries are corrected, it appears that in this case work must be done to change the asymmetrical movement pattern. In the first instance this should focus on the arm action to eliminate the yaw that occurs prior to the recovery of the lower limbs for the kick. It may be that improvement of the arm action leads naturally to improvement in the asymmetries observed with respect to the preparation and performance of the kick. It is evident that the approach described may be used in the diagnosis of the causes of misalignments during swimming that reduce performance potential of individual swimmers. This will enable the design of sound interventional strategies to correct technique and establish bilateral symmetry in strength and flexibility.
In this paper we have presented a method of analysing yaw and establishing its relationship to technique asymmetries. The causes of yaw of an elite swimmer were identified and explained through interpretation of angular momentum and net torque. It has been shown that by quantifying whole body torques, in conjunction with the kinematic movement patterns, the effect of technique asymmetries on body alignment can be assessed. This assessment then contributes to a solid foundation for planning interventions in strength, flexibility, and technique to improve alignment and performance.
| ACKNOWLEDGEMENTS |
The efforts of members of the team at the Centre for Aquatics Research and Education in collecting and digitising a large volume of video data were greatly appreciated. These members included Nuno Oliveir, Tomohiro Gonjo, Chuang-Yuan Chiu, Kostas Kalitsis, Jacki Thow, and Marlies DeClerk. The data presented were part of a project supported by the Sport Institute. |
|
| AUTHOR BIOGRAPHY |
|
 |
Ross H. Sanders |
| Employment: Professor and Head of Exercise and Sport Science at The University of Sydney in the Faculty of Health Sciences. |
| Degree: PhD |
| Research interests: Biomechanics and motor control and learning with specific emphasis on movement asymmetries and rhythms. |
| E-mail: ross.sanders@sydney.edu.au |
| |
 |
Malcolm M. Fairweather |
| Employment: Head of Science and Innovation at the scotlandInstitute of Sport. |
| Degree: PhD |
| Research interests: Application of motor learning and control methodologies and related findings within high performance sport. |
| E-mail: Malcolm.Fairweather@sisport.com |
| |
 |
Alison Alcock |
| Employment: Special Project Scientist at the sport Institute of Sport. |
| Degree: PhD |
| Research interests: Performance analysis and biomechanics |
| E-mail: Alison.Alcock@sisport.com |
| |
 |
Carla B. McCabe |
| Employment: Biomechanist at the School of Sport, Ulster University. |
| Degree: PhD |
| Research interests: Biomechanical analysis of swimming and aquatic exercise. |
| E-mail: c.mccabe@ulster.ac.uk |
| |
|
| |
| REFERENCES |
 Abdel-Aziz Y.I., Karara H.M. (1971) American Society of Photogrammetry Symposium on Close Range Photogrammetry; 1971 Jan 26-29: Falls Church (VA). Direct linear transformation from comparator coordinates into object space coordinates in close range photogrammetry. American Society of Photogrammetry. |
 Bartlett R. (1997) . Introduction to Sports Biomechanics. London. E & FN Spon. |
 Campenella B., Mattacola C.G., Kimura I.F. (2000) Effect of visual feedback and verbal encouragement on concentric quadriceps and hamstrings peak torque of males and females. Isokinetics and Exercise Science, 8, 1-6. |
 Cappaert J.M., Keskinen K., Komi P., Hollander A.P. (1998) Biomechanics and Medicine in Swimming VIII, Proceedings of the VIII International Symposium on Biomechanics and Medicine in Swimming. Biomechanics of swimming analysed by three-dimensional techniques. Jyväskylä (Finland). University of Jyväskylä Press. |
 Carson P.A. (1999) Case Report: The rehabilitation of a competitive swimmer with an asymmetrical movement pattern. Manual Therapy 4, 110-106. |
 Castro F., Minghelli F., Floss J., Guimaraes A., Chatard J.C. (2003) Biomechanics and Medicine in Swimming IX. Body roll angles in front crawl swimming at different velocities. St Etienne. University of St Etienne Publications. |
 Castro F.A.S., Vilas-Boas J.P., Guimaraes A.C.S. (2006) Effect of swimming intensity and breathing in front crawl body roll angles for swimmers and triathletes. Brazilian Journal of Biomechanics 7, 85-90. |
 Collins D., Morriss C., Trower J. (1999) Getting it back: A case study of skill recovery in an elite athlete. The Sport Psychologist 13, 288-298. |
 Counsilman J.E. (1973) The Science of Swimming. Englewood Cliffs N.J. Prentice-Hall. , -. |
 Czabanski B., Koszcyc T., Terauds J., Bedingfield E.W. (1979) Swimming III. Relationship of stroke asymmetry and speed of breaststroke swimming. Baltimore. University Park Press. |
 Dapena J. (1978) A method to determine the angular momentum of a human body about three orthogonal axes passing through its center of gravity. Journal of Biomechanics 11, 251-256. |
 Dapena J. (1980) Mechanics of rotation in the Fosbury-flop. Medicine and Science in Sports and Exercise 12, 45-53. |
 Deffeyes J., Sanders R.H., Wang Q. (2005) Proceedings of XXIII International Symposium on Biomechanics in Sports. Elliptical zone body segment modelling software: digitising, modelling and body segment parameter calculation. Beijing. The China Institute of Sports Science. |
 Feiring D.C., Ellenbecker T.S., Derscheid G.L. (1990) Test-retest reliability of the Biodex Isokinetic Dynamometer. Journal of Orthopaedic and Sports Physical Therapy 11, 298-300. |
 Figueiredo P, Sanders R H, Gorski T, Vilas-Boas J., Fernandes R. (2013) Kinematic and electromyographic changes during 200m front crawl at race pace, International. Journal of Sports Medicine 34, 49-55. |
 Figueiredo P., Seifert L., Vilas-Boas J.P., Fernandes R.J. (2012) Individual profiles of spatio-temporal coordination in high intensity swimming. Human Movement Science 31, 1200-1212. |
 Girold S., Calmels P., Maurin D., Milhau N. (2006) Assisted and resisted sprint training in swimming. Journal of Strength and Conditioning Research/ National Strength & Conditioning Association 20, 547-554. |
 Girold S., Maurin D., Dugué B., Chatard J.-C., Millet G. (2007) Effects of dry-land vs. resisted- and assisted-sprint exercises on swimming sprint performances. Journal of Strength and Conditioning Research / National Strength & Conditioning Association 21, 599-605. |
 Hay J.G. (1993) . The Biomechanics of Sports Techniques. Englewood Cliff, NJ. Prentice-Hall Inc. |
 Jensen R.K. (1978) Estimation of the biomechanical properties of three body types using a photogrammetric method. Journal of Biomechanics , 349-358. |
 Kadaba M.P., Ramakrishnan M.E., Wootten J., Gainey G., Gorton G., Cochran G.V.B. (1989) Repeatability of kinematic, kinetic, and electromyographic data in normal adult gait. Journal of Orthopaedic Research 7, 849-860. |
 Lephart S.M., Ferris C.M., Riemann B.L., Myers J.B., Fu F.H. (2002) Gender Differences in Strength and Lower Extremity Kinematics during Landing. Clinical Orthopaedics and Related Research 401, 162-169. |
 Lui Q, Hay J.G., Andrews J.G. (1993) Body roll and handpath in freestyle swimming: an experimental study. Journal of Applied Biomechanics 9, 238-253. |
 Lund H., Søndergaard K., Zachariassen T., Christensen R., Bülow P., Henriksen M., Bliddal H. (2005) Learning effect of isokinetic measurements in healthy subjects, and reliablity and comparability of Biodex and Lido dynamometers. Clinical Physiology and Functional Imaging 25, 75-82. |
 Maglischo E.W. (2003) Swimming Fastest. Champaign, Il.. Human Kinetics Publishers. |
 Mayer F., Horstmann T., Bäurle W., Grau S., Handel M., Dickhuth H.H. (2001) Diagnostics with isokinetic devices in shoulder measurements - potentials and limits. Isokinetics and Exercise Science 9, 19-25. |
 McCleary R.W., Andersen J.C. (1992) Test-retest reliability of reciprocal isokinetic knee extension and flexion peak torque measurements. Journal of Athletic Training 27, 362-365. |
 Miyashita M., Kanehisa H. (1979) Dynamic peak torque related to age, sex, and performance. The Research Quarterly 50, 249-255. |
 Payton C., Baltzopoulos V., Bartlett R. (2002) Contributions of rotations of the trunk and upper extremity to hand velocity during front crawl swimming. Journal of Applied Biomechanics 18, 243-256. |
 Payton C., Sanders R.H., Seifert L., Chollet D., Mujika I. (2011) World Book of Swimming: From Science to Performance. Body roll in front crawl swimming. New York. Nova Science Publishers. |
 Payton C.J., Bartlett R.M., Baltzopoulos V., Coombs R. (1999) Upper extremity kinematics and body roll during preferred-side breathing and breath-holding front crawl swimming. Journal of Sports Sciences 17, 689-696. |
 Payton C.J., Hay J.G., Mullineaux D.R. (1997) The effect of body roll on hand speed and hand path in front crawl swimming-A simulation study. Journal of Applied Biomechanics 13, 300-315. |
 Psycharakis S., Sanders R.H. (2008) Shoulder and hip roll changes during 200-m front-crawl swimming. Medicine and Science in Sports and Exercise 40, 2129-2136. |
 Psycharakis S.G., McCabe C.B. (2011) Shoulder and hip roll differences between breathing and non-breathing conditions in front crawl swimming. Journal of Biomechanics 44, 1752-1756. |
 Psycharakis S.G., Sanders R., Mill F., Wang Q. (2005) Proceedings of XXIII International Symposium on Biomechanics in Sports. A Calibration Frame for 3D Swimming Analysis. Beijing. The China Institute of Sports Science. |
 Psycharakis S.G., Sanders R.H. (2008) Shoulder and hip roll changes during 200m front crawl swimming. Medicine and Science in Sports and Exercise 40, 2129-2136. |
 Psycharakis S.G., Sanders R.H. (2010) Body roll in swimming: A review. Journal of Sports Sciences 28, 229-236. |
 Sanders R. (1999) Hydrodynamic characteristics of a swimmer’s hand. Journal of Applied Biomechanics 15, 3-26. |
 Sanders R.H. (2013) How do asymmetries affect swimming performance?. Journal of Swimming Research 21, -. |
 Sanders R.H., Psycharakis S.G. (2009) Rolling rhythms in front crawl swimming with six-beat kick. Journal of Biomechanics 42, 273-279. |
 Sanders R.H., Thow J., Alcock A., Fairweather M., Riach I., Mather F. (2012) How can asymmetries in swimming be measured?. Journal of Swimming Science 19, -. |
 Sanders R.H., Thow J., Fairweather M. (2011) Asymmetries in swimming: Where do they come from?. Journal of Swimming Science 18, -. |
 Seifert L, Chehensse A., Torney-Chollet C, Lemaitre F., Chollet D. (2008) Effect of breathing pattern on arm coordination symmetry in front crawl. Journal of Strength and Conditioning Research 22, 1670-1676. |
 Seifert L., Chollet D., Allard P. (2005) Arm coordination symmetry and breathing effect in front crawl. Human Movement Science 24, 234-256. |
 Stickley C.D., Hetzler R.K., Freemyer B.G., Kimura I.F. (2008) Isokinetic peak torque ratios and shoulder injury history in adolescent female volleyball athletes. Journal of Athletic Training 43, 571-577. |
 Tourney-Chollet C., Seifert L., Chollet D. (2009) Effect of force symmetry on coordination in front crawl. International Journal of Sports Medicine 30, 182-187. |
 Yanai T. (2004) Buoyancy is the primary source of generating body roll in front crawl swimming. Journal of Biomechanics 37, 605-612. |
|
| |
|
|
|
|

